题目内容
10.某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完;由于该书畅销,第二次购书时,每本书的进价是第一次进价的1.2倍,他用1500元所购该书数量比第一次多10本;当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.(1)求出第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
分析 (1)设第一次购书的单价为x元,根据第一次用1200元购书若干本,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,列出方程,求出x的值即可得出答案;
(2)根据(1)先求出第一次和第二次购书数目,再根据卖书数目×(实际售价-当次进价)求出二次赚的钱数,再分别相加即可得出答案.
解答 解:(1)设第一次购书的单价为x元,则第二次购书的进价为1.2x元.
根据题意得:$\frac{1200}{x}$+10=$\frac{1500}{1.2x}$,
解得:x=5.
经检验,x=5是原方程的解,
答:第一次购书的进价是5元;
(2)第一次购书为$\frac{1200}{5}$=240(本)
第二次购书为240+10=250(本),
第一次赚钱为240×(7-5)=480(元),
第二次赚钱为200×(7-5×1.2)+50×(7×0.4-5×1.2)=40(元),
所以两次共赚钱480+40=520(元),
答:该老板两次售书总体上是赚钱了,共赚了520元.
点评 此题考查了分式方程的应用,掌握这次活动的流程,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
5.下列多项式不能用平方差分解因式的是( )
| A. | 0.36a2-0.04b2 | B. | x2-16 | C. | -a2+b2+c2 | D. | -x2+y2 |
2.已知A(x1,y1)、B(x2,y2)是函数y=-2x2+m(m是常数)图象上的两个点,如果x1<x2<0,那么y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1,y2的大小不能确定 |




 如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=120°,射线OC的方向是北偏东80°.
如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=120°,射线OC的方向是北偏东80°.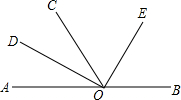 如图,O为直线AB上一点,∠AOC=46°,OD平分∠AOC,∠DOE=90°,
如图,O为直线AB上一点,∠AOC=46°,OD平分∠AOC,∠DOE=90°, 已知抛物线G1:y=a(x-h)2+2的对称轴为x=-1,且经过原点.
已知抛物线G1:y=a(x-h)2+2的对称轴为x=-1,且经过原点. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=3,DE=5,则线段EC的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=3,DE=5,则线段EC的长为( )