题目内容
关于x的方程x2+kx+k-1=0的根的情况描述正确的是( )
| A、k为任何实数,方程都没有实数根 |
| B、k为任何实数,方程都有两个实数根 |
| C、k为任何实数,方程都有两个相等的实数根 |
| D、根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
考点:根的判别式
专题:计算题
分析:先计算根的判别式得到△=k2-4(k-1),变形得到△═k2-4k+4=(k-2)2,由于(k-2)2,≥0,即△≥0,根据△的意义可判断方程根的情况.
解答:解:△=k2-4(k-1)
=k2-4k+4
=(k-2)2,
∵(k-2)2,≥0,即△≥0,
∴原方程有两个实数根,当k=2时,方程有两个相等的实数根.
故选B.
=k2-4k+4
=(k-2)2,
∵(k-2)2,≥0,即△≥0,
∴原方程有两个实数根,当k=2时,方程有两个相等的实数根.
故选B.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
由于换季清库,某服装原价为168元,连续两次降价a%后售价为136元,下列所列方程中正确的是( )
| A、168 (1+a%)2=136 |
| B、168 (1-a2%)=136 |
| C、168 (1-2a%)=136 |
| D、168 (1-a%)2=136 |
等腰三角形的一边等于5,一边等于12,则它的周长是( )
| A、22 | B、29 |
| C、22或29 | D、17 |
下列平面图形中,属于中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,三内角皆小于120°的三角形,分别以AB,BC,CA为边,向三角形外侧做正三角形ABD,ACE,BCF,然后连接AF,BE,CD,这三线交于一点O,那么下列结论中
如图,三内角皆小于120°的三角形,分别以AB,BC,CA为边,向三角形外侧做正三角形ABD,ACE,BCF,然后连接AF,BE,CD,这三线交于一点O,那么下列结论中 如图,在菱形ABCD中,对角线长度分别为6和8,P为直线AB、CD之间的任一点,分别连接PA、PB、PC、PD,则△PAB和△PCD的面积之和为( )
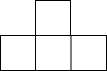
如图,在菱形ABCD中,对角线长度分别为6和8,P为直线AB、CD之间的任一点,分别连接PA、PB、PC、PD,则△PAB和△PCD的面积之和为( ) 从不同方向观察同一物体时,可能看到不同的图形.其中,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.请问,下面哪一幅图是右面这个几何体的左视图?( )
从不同方向观察同一物体时,可能看到不同的图形.其中,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.请问,下面哪一幅图是右面这个几何体的左视图?( )


 如图,AB=AD,BC=DC,E、F在AC上,
如图,AB=AD,BC=DC,E、F在AC上,