题目内容
在下面过程中的横线上填空.
已知:如图,BC∥EF,BC=EF,AD=BE.求证:AC=DF.
解:∵BC∥EF
∴∠ABC=∠ E
又∵AD=BE(已知)
∴AB= DE
在△ABC和△DEF中
![]()
∵ =
=
∴△ABC≌ △DEF
∴ = .

考点:全等三角形的判定与性质。
专题:推理填空题。
分析:由平行证明同位角∠ABC=∠E,由AD=BE可推出AB=DE,又BC=EF,利用“SAS”定理证明△ABC≌△DEF,可得AC=CF.
解答:证明:∵BC∥EF
∴∠ABC=∠E
又∵AD=BE(已知)
∴AB=DE
在△ABC和△DEF中
∵BC=EF,∠ABC=∠E,AB=DE,
∴△ABC≌△DEF(SAS)
∴AC=DF.
点评:三角形全等的判定是中考的热点,一般以考查三角形全等![]() 的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由. 的横线上填空,并在括号内注明理由.
的横线上填空,并在括号内注明理由. 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由.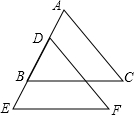 在下面过程中的横线上填空.
在下面过程中的横线上填空. 17、在下面过程中的横线上填空,并在括号内注明理由.如图,已知∠B=∠C,AD=AE,说明DB与EC相等.
17、在下面过程中的横线上填空,并在括号内注明理由.如图,已知∠B=∠C,AD=AE,说明DB与EC相等.