题目内容
 17、在下面过程中的横线上填空,并在括号内注明理由.如图,已知∠B=∠C,AD=AE,说明DB与EC相等.
17、在下面过程中的横线上填空,并在括号内注明理由.如图,已知∠B=∠C,AD=AE,说明DB与EC相等.解:在△ABE和△ACD中
∠B=
∠C
(已知)∠A=∠A
AD=AE (已知)∴△ABE≌△ACD
AAS
∴AB=AC
又∵AD=AE
∴AB-AD=AC-AE,
即DB=EC.
分析:根据证明△ABE≌△ACD,寻找三角形全等的条件,需要结合已知和图形条件求解.
解答:解:在△ABE和△ACD中,
∠B=∠C(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴△ABE≌△ACD(AAS)
∴AB=AC(全等三角形,对应边相等)
又∵AD=AE,
∴AB-AD=AC-AE,
即DB=EC.
故答案为:∠C,∠A,AAS,AC.
∠B=∠C(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴△ABE≌△ACD(AAS)
∴AB=AC(全等三角形,对应边相等)
又∵AD=AE,
∴AB-AD=AC-AE,
即DB=EC.
故答案为:∠C,∠A,AAS,AC.
点评:本题考查了全等三角形的判定与性质.关键是由已知条件,图形条件寻找证明三角形全等的条件.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由. 的横线上填空,并在括号内注明理由.
的横线上填空,并在括号内注明理由. 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由.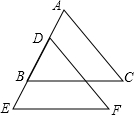 在下面过程中的横线上填空.
在下面过程中的横线上填空.