题目内容
如图所示,直线AB,CD,EF相交于点O,∠DOB的度数是它余角的2,∠AOE=2∠DOF,OG⊥AB.
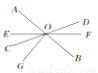
求：(1)∠DOB的度数;
(2)∠BOF的度数;
(3)∠EOG的度数.
(1)∠DOB=60°;(2)∠BOF =40°; (3)∠EOG=50°. 【解析】试题分析: （1）首先根据垂直定义可得∠GOB=90°，根据平角定义可得∠COG+∠DOB=90°，再根据∠DOB是它余角的2倍可得∠DOB+∠DOB=90°，进而可算出∠DOB的度数； （2）首先根据对顶角相等可得∠AOC的度数，再根据∠AOE=2∠DOF可得3∠COE=60°，继而可得∠COE=2...
练习册系列答案
相关题目
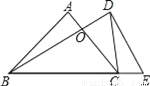
将一副直角三角板如图摆放，等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD．
求证：△CDO是等腰三角形．
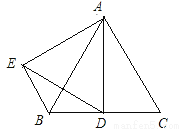
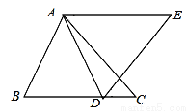
如图：△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE=BD．
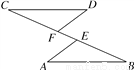
如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
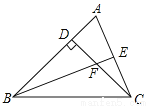
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．
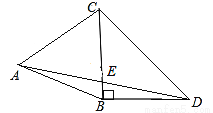
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
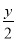＋1＝0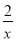
＋3＝0 D. 2y2＝8
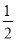，且经过点(2，0).下列说法：①abc<0；②a+b=0；③4a+2b+c<0；④若(-2，y1)，(
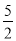，y2)是抛物线上的两点，则y1＜y2，其中说法正确的是( ) 
