题目内容

3．已知⊙O1的半径r1=6，⊙O2的半径为r2，圆心距O1O2=3，如果⊙O1与⊙O2有交点，那么r2的取值范围是（　　）
A．r2≥3B．r2≤9C．3＜r2＜9D．3≤r2≤9

分析 由⊙O1的半径r1=6，⊙O2的半径为r2，圆心距O1O2=3，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系，可求得内切时，r2的值，继而求得答案．

解答 解：∵⊙O1的半径r1=6，⊙O2的半径为r2，圆心距O1O2=3，
∴若⊙O1与⊙O2内切，则r2=3或r2=9，
∵⊙O1与⊙O2有交点，
∴r2的取值范围是：3≤r2≤9．
故选D．

点评 此题考查了圆与圆的位置关系．注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．

练习册系列答案
相关题目
13．计算：
（1）${（{\frac{1}{2}}）^3}×{（{\frac{1}{2}}）^2}×{（{-\frac{1}{2}}）^4}×（{\frac{1}{2}}）$
（2）${[{{{（{-\frac{1}{2}}）}^n}}]^2}+{（{-\frac{1}{2}}）^{2n-1}}×\frac{1}{2}$（n是正整数）
14．计算：
（1）2-2+|-$\sqrt{12}$|-2cos30°-（π+$\sqrt{3}$）0
（2）（$\frac{a+2}{{a}^{2}-2a}$-$\frac{a-1}{{a}^{2}-4a+4}$）$÷\frac{a-4}{a}$．
11．已知点A（x1，y1），B（x2，y2），C（x3，y3）都在反比例函数y=-$\frac{1}{x}$的图象上，且x1＜x2＜0＜x3，则y1，y2，y3的大小关系是y2＞y1＞y3．
18．下列各数是无理数的是（　　）
A．$\frac{22}{7}$B．$\sqrt{5}$C．$\sqrt{9}$D．16
8．某服装厂从20万件同类产品中随机抽取了100件进行质检，发现其中有2件不合格，那么你估计该厂这20万件产品中合格品约为19.6万件．
15．化简$\frac{{x}^{2}-1}{x}÷\frac{x+1}{x}$的结果（　　）
A．x-1B．xC．$\frac{1}{x}$D．$\frac{1}{x-1}$
12．某物流公司要把3000吨货物从M市运到W市．（每日的运输量为固定值）
（1）从运输开始，每天运输的货物吨数y（单位：吨）与运输时间x（单位：天）之间有怎样的函数关系式？
（2）因受到沿线道路改扩建工程影响，实际每天的运输量比原计划少20%，以致推迟1天完成运输任务，求原计划完成运输任务的天数．
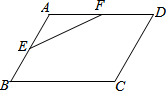1．如图，在?ABCD中，E、F分别是AB、AD的中点，若△AEF的面积为5cm2，则?ABCD的面积是40cm2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网