Question

1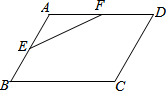．如图，在?ABCD中，E、F分别是AB、AD的中点，若△AEF的面积为5cm²，则?ABCD的面积是40cm²．

Answer 1

分析 连结BD，根据三角形中位线定理得出EF∥BD，EF=$\frac{1}{2}$BD，那么△AEF∽△ABD，利用相似三角形面积比等于相似比的平方求出S_△ABD=4S_△AEF=20cm²，根据平行四边形的性质得出AD∥BC，AD=BC，由等底等高的三角形面积相等得出S_△CBD=S_△ADB=20cm²，于是S_?ABCD=40cm²．

解答 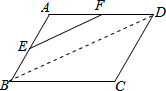解：如图，连结BD．
∵E、F分别是AB、AD的中点，
∴EF∥BD，EF=$\frac{1}{2}$BD，
∴△AEF∽△ABD，
∴$\frac{{S}_{△AEF}}{{S}_{△ABD}}$=（$\frac{EF}{BD}$）²=$\frac{1}{4}$，
∴S_△ABD=4S_△AEF=20cm²，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴S_△CBD=S_△ADB=20cm²，
∴S_?ABCD=40cm²．
故答案为40cm²．

点评 本题考查了相似三角形的判定与性质，三角形中位线定理以及平行四边形的性质，作出辅助线求出S_△ABD=4S_△AEF=20cm²是解题的关键．