题目内容
顺次连结正方形各边中点所成的四边形的面积与原正方形的面积之比为( )
A、1:
| ||
B、1:
| ||
| C、1:3 | ||
| D、1:2 |
考点:中点四边形
专题:几何图形问题
分析:根据题意作图,利用中位线定理可证明顺次连接正方形四边中点所得的四边形的与原正方形相似,且相似比是
:2,所以可求得的四边形的面积与原正方形的面积的比为1:2.
| 2 |
解答: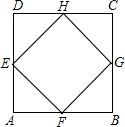 解:如图:∵四边形ABCD是正方形,
解:如图:∵四边形ABCD是正方形,
∴∠A=∠B=90°,AD=AB=BC=CD.
∵E,F,G,H是正方形各边的中点,
∴AE=AF=BF=BG,
在△AEF与△BFG中,
,
∴△AEF≌△BFG(ASA),
∴∠EFA=∠GFB=45°
∴∠EFG=90°,EF=FG
同理:EF=FG=GH=EH
∴四边形EFGH是正方形
∴四边形ABCD∽四边形EFGH
设AB=2x,则AF=x,EF=
x
∴所得的四边形与原正方形的相似比为
:2
∴所得的四边形的面积与原正方形的面积的比为1:2.
故选:D.
 解:如图:∵四边形ABCD是正方形,
解:如图:∵四边形ABCD是正方形,∴∠A=∠B=90°,AD=AB=BC=CD.
∵E,F,G,H是正方形各边的中点,
∴AE=AF=BF=BG,
在△AEF与△BFG中,
|
∴△AEF≌△BFG(ASA),
∴∠EFA=∠GFB=45°
∴∠EFG=90°,EF=FG
同理:EF=FG=GH=EH
∴四边形EFGH是正方形
∴四边形ABCD∽四边形EFGH
设AB=2x,则AF=x,EF=
| 2 |
∴所得的四边形与原正方形的相似比为
| 2 |
∴所得的四边形的面积与原正方形的面积的比为1:2.
故选:D.
点评:此题考查了四边形、相似多边形的性质,相似多边形的面积比等于相似比的平方.

练习册系列答案
相关题目
已知
是方程2x-ay=3的一组解,那么a的值为( )
|
| A、-1 | B、3 | C、-3 | D、-15 |
如果点P(3,y)在第四象限,则y的取值范围是( )
| A、y>0 | B、y<0 |
| C、y≥0 | D、y≤0 |
如果座位表上“5列2行”记作(5,2),那么(4,3)表示( )
| A、3列5行 | B、5列3行 |
| C、4列3行 | D、3列4行 |
 如图所示的数轴上,点A与点C关于点B对称,A、B两点的对应的实数是-
如图所示的数轴上,点A与点C关于点B对称,A、B两点的对应的实数是-| 3 |
A、1+
| ||
B、2+
| ||
C、2
| ||
D、2
|
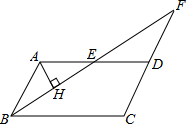 如图,?ABCD中,BC=6,∠ABC的平分线与CD的延长线相交于点F,与AD交于点E,且点E为AD边的中点,过点A作BF的垂线,垂足为H.若AH=2,则BF的长为
如图,?ABCD中,BC=6,∠ABC的平分线与CD的延长线相交于点F,与AD交于点E,且点E为AD边的中点,过点A作BF的垂线,垂足为H.若AH=2,则BF的长为 如图,直线y=kx+b与反比例函数
如图,直线y=kx+b与反比例函数
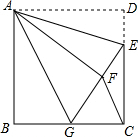 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论: