题目内容
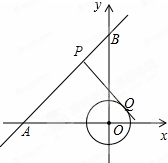 如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为考点:圆的综合题
专题:
分析:连接OP.根据勾股定理知PQ2=OP2-OQ2,当OP⊥AB时,线段OP最短,即线段PQ最短.
解答:解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;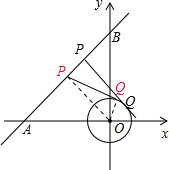
根据勾股定理知PQ2=OP2-OQ2,
∵当PO⊥AB时,线段PQ最短;
又∵A(-6,0)、B(0,6),
∴OA=OB=6,
∴AB=
=6
∴OP=
AB=3
,
∵OQ=3,
∴PQ=
=3,
故答案为:3.
∵PQ是⊙O的切线,
∴OQ⊥PQ;

根据勾股定理知PQ2=OP2-OQ2,
∵当PO⊥AB时,线段PQ最短;
又∵A(-6,0)、B(0,6),
∴OA=OB=6,
∴AB=
| 62+62 |
| 2 |
∴OP=
| 1 |
| 2 |
| 2 |
∵OQ=3,
∴PQ=
| PO2-OQ2 |
故答案为:3.
点评:本题考查了切线的判定与性质、坐标与图形性质以及矩形的性质等知识点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角来解决有关问题.

练习册系列答案
相关题目
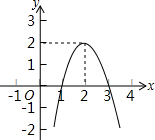 二次函数y=ax2+bx+c(a为常数,a≠0)的图象如图,一元二次方程ax2+bx+c=2根的情况为( )
二次函数y=ax2+bx+c(a为常数,a≠0)的图象如图,一元二次方程ax2+bx+c=2根的情况为( )| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法判断 |
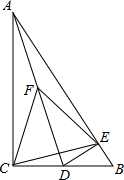 已知:如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,D是BC上任意一点,过点D作DE⊥AB于E,F是AD的中点,连接CF、EF、CE,求证:△CEF是正三角形.
已知:如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,D是BC上任意一点,过点D作DE⊥AB于E,F是AD的中点,连接CF、EF、CE,求证:△CEF是正三角形. 如图,在Rt△ABC中,∠C=90°,∠A=30°,斜边AB=2,求:
如图,在Rt△ABC中,∠C=90°,∠A=30°,斜边AB=2,求: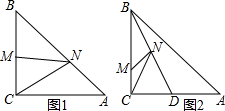 在△ABC中,∠ACB=90°,AC=BC=2,M是BC边上一点.
在△ABC中,∠ACB=90°,AC=BC=2,M是BC边上一点.