题目内容
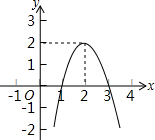 二次函数y=ax2+bx+c(a为常数,a≠0)的图象如图,一元二次方程ax2+bx+c=2根的情况为( )
二次函数y=ax2+bx+c(a为常数,a≠0)的图象如图,一元二次方程ax2+bx+c=2根的情况为( )| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法判断 |
考点:抛物线与x轴的交点
专题:
分析:由图可知ax2+bx+c-2=0的根的情况即图中图象和x轴交点的横坐标,为两个不相等的正数,再根据y=ax2+bx+c-2,相当于函数y=ax2+bx+c的图象向下平移2个单位,由此可得出结论.
解答:解:∵函数的顶点的纵坐标为2,
∴直线y=2与函数图象只有一个交点,
∴y=ax2+bx+c-2,相当于函数y=ax2+bx+c的图象向下平移2个单位,
∴方程ax2+bx+c-2=0有两个相等的实数根,.
故选A.
∴直线y=2与函数图象只有一个交点,
∴y=ax2+bx+c-2,相当于函数y=ax2+bx+c的图象向下平移2个单位,
∴方程ax2+bx+c-2=0有两个相等的实数根,.
故选A.
点评:本题考查了二次函数与一元二次方程的知识,解题的关键是通过看图象直线y=2与抛物线的交点个数.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,甲、乙、丙、丁四人分别面对面坐在一张四方形桌子旁边.桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“
如图,甲、乙、丙、丁四人分别面对面坐在一张四方形桌子旁边.桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“ ”,丙说他看到的是“
”,丙说他看到的是“ ”,丁说他看到的是“9”则下列正确的是( )
”,丁说他看到的是“9”则下列正确的是( )| A、甲在丁的对面,乙在甲的左边,丙在丁的右边 |
| B、丙在乙的对面,丙的左边是甲,右边是丁 |
| C、甲在乙的对面,甲的右边是丙,左边是丁 |
| D、甲在丁的对面,乙在甲的右边,丙在丁的右边 |
 如图是统计学生跳绳情况的频数分布直方图,根据这个图回答下列问题:
如图是统计学生跳绳情况的频数分布直方图,根据这个图回答下列问题: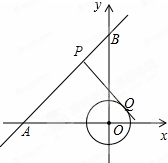 如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为