题目内容
判断方程x2-y2=1990是否有整数解,并说明理由.
考点:非一次不定方程(组)
专题:
分析:由平方差公式可知x2-y2=(x+y)(x-y),(x+y)与 (x-y)是同奇或者同偶,将1990分为两个数的积,分别解方程组即可.
解答:解:∵1990=1×1990=(-1)×(-1990)=2×995=(-2)×(-995)=5×398=(-5)×(-398)=10×199=(-10)×(-199),
∴(x+y),(x-y)同奇或者同偶,分别可取下列数对
(1,1990),(1990,1),(-1,-1990),(-1990,-1),
(2,995)、(995,2)、(-2,-995)、(-995,-2),
(5,398)、(398,5)、(-5,-398)、(-398,-5),
(10,199),(199,10),(-10,-199),(-199,-10),
因为它们都不是同奇或者同偶,
故方程x2-y2=1990没有整数解.
∴(x+y),(x-y)同奇或者同偶,分别可取下列数对
(1,1990),(1990,1),(-1,-1990),(-1990,-1),
(2,995)、(995,2)、(-2,-995)、(-995,-2),
(5,398)、(398,5)、(-5,-398)、(-398,-5),
(10,199),(199,10),(-10,-199),(-199,-10),
因为它们都不是同奇或者同偶,
故方程x2-y2=1990没有整数解.
点评:本题主要考查非一次不定方程的知识点,解答本题的关键是掌握平方差公式的实际运用,应明确两整数之和与两整数之差的奇偶性相同.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,甲、乙、丙、丁四人分别面对面坐在一张四方形桌子旁边.桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“
如图,甲、乙、丙、丁四人分别面对面坐在一张四方形桌子旁边.桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“ ”,丙说他看到的是“
”,丙说他看到的是“ ”,丁说他看到的是“9”则下列正确的是( )
”,丁说他看到的是“9”则下列正确的是( )| A、甲在丁的对面,乙在甲的左边,丙在丁的右边 |
| B、丙在乙的对面,丙的左边是甲,右边是丁 |
| C、甲在乙的对面,甲的右边是丙,左边是丁 |
| D、甲在丁的对面,乙在甲的右边,丙在丁的右边 |

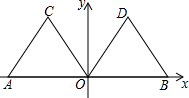 如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称都可以得到△OBD.
如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称都可以得到△OBD.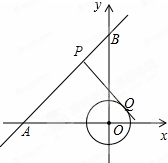 如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为 如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的
如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的