题目内容
8.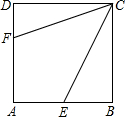 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3$\sqrt{5}$,且∠ECF=45°,则CF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3$\sqrt{5}$,且∠ECF=45°,则CF的长为( )| A. | 2$\sqrt{10}$ | B. | 3$\sqrt{5}$ | C. | $\frac{5}{3}\sqrt{10}$ | D. | $\frac{10}{3}\sqrt{5}$ |
分析 首先延长FD到G,使DG=BE,利用正方形的性质得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性质易得△GCF≌△ECF,利用勾股定理可得AE=3,设AF=x,利用GF=EF,解得x,利用勾股定理可得CF.
解答 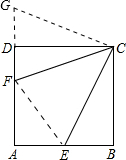 解:如图,延长FD到G,使DG=BE;
解:如图,延长FD到G,使DG=BE;
连接CG、EF;
∵四边形ABCD为正方形,
在△BCE与△DCG中,
$\left\{\begin{array}{l}{CB=CD}\\{∠CBE=∠CDG}\\{BE=DG}\end{array}\right.$,
∴△BCE≌△DCG(SAS),
∴CG=CE,∠DCG=∠BCE,
∴∠GCF=45°,
在△GCF与△ECF中,
$\left\{\begin{array}{l}{GC=EC}\\{∠GCF=∠ECF}\\{CF=CF}\end{array}\right.$,
∴△GCF≌△ECF(SAS),
∴GF=EF,
∵CE=3$\sqrt{5}$,CB=6,
∴BE=$\sqrt{C{E}^{2}-C{B}^{2}}$=$\sqrt{(3\sqrt{5})^{2}-{6}^{2}}$=3,
∴AE=3,
设AF=x,则DF=6-x,GF=3+(6-x)=9-x,
∴EF=$\sqrt{A{E}^{2}+{x}^{2}}$=$\sqrt{9+{x}^{2}}$,
∴(9-x)2=9+x2,
∴x=4,
即AF=4,
∴GF=5,
∴DF=2,
∴CF=$\sqrt{C{D}^{2}+D{F}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
故选:A.
点评 本题主要考查了全等三角形的判定及性质,勾股定理等,构建全等三角形,利用方程思想是解答此题的关键.

 如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )
如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )| A. | 70° | B. | 110° | C. | 30° | D. | 150° |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |

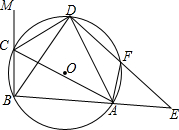 在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为$\widehat{AD}$上-
在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为$\widehat{AD}$上-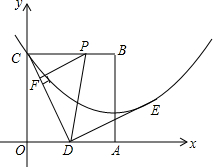 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点. 如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点.
如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点. 如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
如图,四边形ABCD、BEFG均为正方形,连接AG、CE.