题目内容
2.铁路上有东、西两站,甲、乙两列火车同时从东、西站相向出发.假设两列火车各自的速度都是均匀不变的,当两列火车在途中相遇时,甲列车再过1小时就到达西站,而乙列车还需要2小时15分钟才可抵达东站.哪列火车的速度快?它的速度是另一列火车速度的几倍?分析 假设甲、乙两人在O点相遇,甲从A点(东站)出发,乙从B点(西站)出发,设甲的速度为x,乙的速度为y,则相遇时甲走了AO段,乙走了BO段,此时甲、乙所用的时间相同,由时间=路程÷时间可得方程,求出即可.
解答 解:设甲的速度为x,乙的速度为y,则相遇时甲走了AO段,乙走了BO段,
根据题意可得:$\frac{AO}{x}$=$\frac{BO}{y}$,
∵AO等于乙剩下的路程,即乙用2小时15分钟所走的距离,
∴AO=2$\frac{1}{4}$y.
BO等于甲剩下的路程,即甲用1小时所走的距离,
BO=1×x.
将AO,BO代入$\frac{AO}{x}$=$\frac{BO}{y}$,
即$\frac{\frac{9}{4}y}{x}$=$\frac{x}{y}$,
解得:$\frac{9}{4}$y2=x2,
则$\frac{x}{y}$=$\frac{3}{2}$.
答:甲列车速度快,它的速度是另一列火车的$\frac{3}{2}$倍.
点评 此题主要考查了分式方程的应用,根据题意结合行程问题中的基本数量关系,得出两车速度之比是解题关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
11.若点A(a,2-a)在第一象限,a为整数,则a的平方根是( )
| A. | 1 | B. | ±2 | C. | ±1 | D. | 不确定 |
8.已知关于x的方程(k-3)x|k|-1+(2k-3)x+4=0是一元二次方程,则k的值应为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 不能确定 |
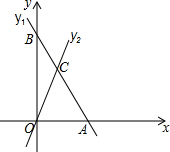 如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).
如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).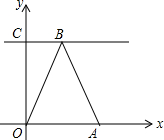 在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$,分别以OA,OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系;
在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$,分别以OA,OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系;