题目内容
 已知△AOD≌△AOE,∠ADO=90°,点B在边DO上,点C在OE的延长线上,且∠AOC=∠BAC=60°.
已知△AOD≌△AOE,∠ADO=90°,点B在边DO上,点C在OE的延长线上,且∠AOC=∠BAC=60°.(1)求证:△ABC是等边三角形;
(2)求证:OB+OC=OA;
(3)若BA=5,OA=7,求△BOC的周长.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:计算题
分析:(1)由已知三角形全等,得到对应角相等,对应边相等,进而得到∠DAB=∠EAC,再由一对直角相等,且夹边AD=AE,利用ASA得到三角形ADB与三角形AEC全等,利用全等三角形对应边相等得到AB=AC,再由∠BAC=60°,利用有一个角为60°的等腰三角形为等边三角形即可得证;
(2)延长OC到F,使得CF=OB,连结AF,根据三角形ABC为等边三角形得到AB=AC,由三角形ADB与三角形AEC全等,利用全等三角形对应角相等得到一对角相等,利用等角的补角相等得到夹角相等,利用SAS得到三角形ABO与三角形ACF全等,进而得到AO=AF,由∠ACF=60°,得到三角形ACF为等边三角形,根据OA=OF,等量代换即可得证;
(3)表示出三角形BOC的周长,等量代换即可求出.
(2)延长OC到F,使得CF=OB,连结AF,根据三角形ABC为等边三角形得到AB=AC,由三角形ADB与三角形AEC全等,利用全等三角形对应角相等得到一对角相等,利用等角的补角相等得到夹角相等,利用SAS得到三角形ABO与三角形ACF全等,进而得到AO=AF,由∠ACF=60°,得到三角形ACF为等边三角形,根据OA=OF,等量代换即可得证;
(3)表示出三角形BOC的周长,等量代换即可求出.
解答: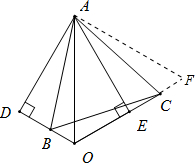 (1)证明:∵△AOD≌△AOE,∠D=90°,
(1)证明:∵△AOD≌△AOE,∠D=90°,
∴∠AOD=∠AOC=60°,∠DAO=∠EAO=30°,AD=AE,
∴∠DAE=60°,
∵∠BAC=60°,
∴∠DAB=∠EAC=60°-∠BAE,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(ASA),
∴AB=AC,
∵∠BAC=60°,
∴△ABC是等边三角形;
(2)证明:延长OC到F,使得CF=OB,连结AF,
∵△ADB≌△AEC,
∴∠ABD=∠ACE,即∠ABO=∠ACF,
在△ABO和△ACF中,
,
∴△ABO≌△ACF(SAS),
∴AO=AF,
∵∠AOF=60°,
∴△AOF是等边三角形,即AO=OF,
∴AO=OB+OC;
(3)解:∵OA=OF=OC+CF=OC+OB,BC=AB,
∴△OBC的周长=OB+OC+BC=OA+BC=OA+AB=12.
 (1)证明:∵△AOD≌△AOE,∠D=90°,
(1)证明:∵△AOD≌△AOE,∠D=90°,∴∠AOD=∠AOC=60°,∠DAO=∠EAO=30°,AD=AE,
∴∠DAE=60°,
∵∠BAC=60°,
∴∠DAB=∠EAC=60°-∠BAE,
在△ADB和△AEC中,
|
∴△ADB≌△AEC(ASA),
∴AB=AC,
∵∠BAC=60°,
∴△ABC是等边三角形;
(2)证明:延长OC到F,使得CF=OB,连结AF,
∵△ADB≌△AEC,
∴∠ABD=∠ACE,即∠ABO=∠ACF,
在△ABO和△ACF中,
|
∴△ABO≌△ACF(SAS),
∴AO=AF,
∵∠AOF=60°,
∴△AOF是等边三角形,即AO=OF,
∴AO=OB+OC;
(3)解:∵OA=OF=OC+CF=OC+OB,BC=AB,
∴△OBC的周长=OB+OC+BC=OA+BC=OA+AB=12.
点评:此题考查了全等三角形的判定与性质,以及等边三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
设一个正方形的边长为1cm,若边长增加2cm,则新正方形的面积增加了( )
| A、6cm2 |
| B、5cm2 |
| C、8cm2 |
| D、7cm2 |
 如图,两张大小相同的长方形纸,各折出7个大小相同且宽度均为1公分的长方形(如BC=1公分).若将两张纸放置使得顶点在A重合,P点落在CD上,则BP=
如图,两张大小相同的长方形纸,各折出7个大小相同且宽度均为1公分的长方形(如BC=1公分).若将两张纸放置使得顶点在A重合,P点落在CD上,则BP= 如图,点P是∠AOB的角平分线上一点,过P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,求点P到OA的距离PD.
如图,点P是∠AOB的角平分线上一点,过P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,求点P到OA的距离PD.

 如图,边长为1的正方形ABCD沿对角线BD向右平移到HEFG,使两正方形重叠部分MEND的面积是ABCD的面积的一半,求平移距离为多少?
如图,边长为1的正方形ABCD沿对角线BD向右平移到HEFG,使两正方形重叠部分MEND的面积是ABCD的面积的一半,求平移距离为多少?