题目内容
设方程x2+2x-1=0的两个实数根为x1、x2,求:
(1)x1+x2;
(2)x1•x2;
(3)x12+x22;
(4)
+
的值.
(1)x1+x2;
(2)x1•x2;
(3)x12+x22;
(4)
| 1 |
| x1 |
| 1 |
| x2 |
考点:根与系数的关系
专题:计算题
分析:(1)、(2)根据根与系数的关系求解;
(3)先利用完全平方公式变形得到x12+x22=(x1+x2)2-2x1x2,然后利用整体代入的方法计算;
(4)先通分,再利用整体代入的方法计算.
(3)先利用完全平方公式变形得到x12+x22=(x1+x2)2-2x1x2,然后利用整体代入的方法计算;
(4)先通分,再利用整体代入的方法计算.
解答:解:(1)x1+x2=-2;
(2)x1•x2=-1;
(3)x12+x22=(x1+x2)2-2x1x2=(-2)2-2×(-1)=6;
(4)
+
=
=
=2.
(2)x1•x2=-1;
(3)x12+x22=(x1+x2)2-2x1x2=(-2)2-2×(-1)=6;
(4)
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| -2 |
| -1 |
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
方程(x-5)(x+1)=x-5的解是( )
| A、x=0 |
| B、x=5 |
| C、x=5或x=--1 |
| D、x=5或x=0 |
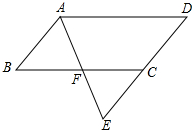 如图所示,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,
如图所示,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F, 如图,已知∠CAB=∠DBA,只要再添加一个条件:
如图,已知∠CAB=∠DBA,只要再添加一个条件: 已知,如图,四边形OABC是正方形,点B的坐标为(2,2),点D在OC边上,△AOD的面积是正方形OABC面积的
已知,如图,四边形OABC是正方形,点B的坐标为(2,2),点D在OC边上,△AOD的面积是正方形OABC面积的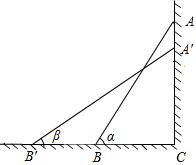 如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα=
如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα=