题目内容
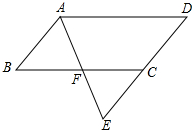 如图所示,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,
如图所示,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
考点:平行四边形的性质,全等三角形的判定与性质,矩形的判定
专题:证明题
分析:(1)根据平行四边形对边相等可得AB=CD,然后求出AB=CE,再根据两直线平行,内错角相等可得∠ABC=∠ECF,然后利用“角角边”证明△ABF和△ECF全等即可;
(2)根据平行四边形的对角相等可得∠ABC=∠D,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AFC=∠ABC+∠BAF,然后求出∠ABC=∠BAF,再根据等角对等边可得AF=BF,根据全等三角形对应边相等可得BF=CF,AF=EF,从而得到AF=BF=EF=CF,再根据对角线互相平分且相等的四边形是矩形证明.
(2)根据平行四边形的对角相等可得∠ABC=∠D,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AFC=∠ABC+∠BAF,然后求出∠ABC=∠BAF,再根据等角对等边可得AF=BF,根据全等三角形对应边相等可得BF=CF,AF=EF,从而得到AF=BF=EF=CF,再根据对角线互相平分且相等的四边形是矩形证明.
解答: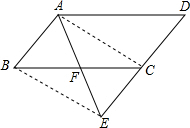 (1)证明:在平行四边形ABCD中,AB=CD,
(1)证明:在平行四边形ABCD中,AB=CD,
∵CE=DC,
∴AB=CE,
∵AB∥CD,
∴∠ABC=∠ECF,
在△ABF和△ECF中,
,
∴△ABF≌△ECF(AAS);
(2)证明:在平行四边形ABCD中,∠ABC=∠D,
所以,∠AFC=∠ABC+∠BAF,
∵∠AFC=2∠D,
∴∠ABC=∠BAF,
∴AF=BF,
∵△ABF≌△ECF,
∴BF=CF,AF=EF,
∴AF=BF=EF=CF,
∴四边形ABEC是矩形.
 (1)证明:在平行四边形ABCD中,AB=CD,
(1)证明:在平行四边形ABCD中,AB=CD,∵CE=DC,
∴AB=CE,
∵AB∥CD,
∴∠ABC=∠ECF,
在△ABF和△ECF中,
|
∴△ABF≌△ECF(AAS);
(2)证明:在平行四边形ABCD中,∠ABC=∠D,
所以,∠AFC=∠ABC+∠BAF,
∵∠AFC=2∠D,
∴∠ABC=∠BAF,
∴AF=BF,
∵△ABF≌△ECF,
∴BF=CF,AF=EF,
∴AF=BF=EF=CF,
∴四边形ABEC是矩形.
点评:本题考查了平行四边形的性质,全等三角形的判定与性质,矩形的判定,熟练掌握三角形全等的判定方法是解题的关键,考虑利用对角线的关系判断矩形是解题的关键.

练习册系列答案
相关题目
如果存入500元记为+500元,那么支出300元记为( )
| A、+300元 |
| B、-300元 |
| C、+200元 |
| D、-200元 |
把(-5)-(+3)-(-7)+(-2)写成省略加号和括号的形式,正确的是( )
| A、-5-3+7-2 |
| B、5-3-7-2 |
| C、5-3+7-2 |
| D、5+3-7-2 |
 如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.
如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.