题目内容
如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E。
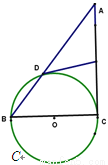
(1)求证:AC是⊙O的切线;
(2)若AD:DB=3:2,AC=15,求⊙O的直径。
(1)连接OD、CD,先根据切线的性质得到OD⊥DE,即∠1+∠2=90°,再根据圆周角定理可得∠BDC=90°,再结合E为AC的中点,根据直角三角形的性质可得DE=CE=AE=AC,即得∠2=∠3,根据元的基本性质可得∠1=∠4,即得∠3+∠4=∠1+∠2=90°,从而证得结论;(2) 【解析】 试题分析:(1)连接OD、CD,先根据切线的性质得到OD⊥DE,即∠1+∠2=90°,再...
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目


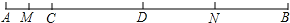
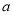 、
、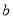 、
、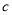 、
、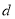 的位置如图,如果
的位置如图,如果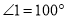 ,
, 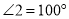 ,
, 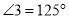 ,那么
,那么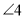 等于( )
等于( )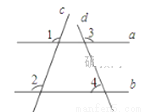
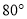 B.
B. 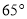 C.
C. 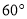 D.
D. 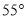

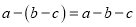 ; (2)
; (2)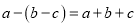 ;
;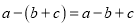 ; (4)
; (4)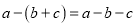 .
. 在实数范围内有意义,则取值范围是________.
在实数范围内有意义,则取值范围是________.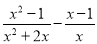 , B=2x2+4x+2.
, B=2x2+4x+2.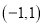 在第__________ 象限.
在第__________ 象限.