题目内容
10.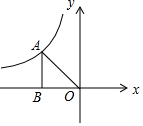 如图,点A在反比例函数y=$\frac{m-3}{x}$的图象上,连接OA,作AB⊥x轴,垂足为B,点A的坐标为(-2,n),OA=2$\sqrt{2}$.
如图,点A在反比例函数y=$\frac{m-3}{x}$的图象上,连接OA,作AB⊥x轴,垂足为B,点A的坐标为(-2,n),OA=2$\sqrt{2}$.(1)求m的值;
(2)若点C(a,y1),D(a+2,y2)(a>0)在这个函数的图象上,试比较y1与y2的大小.
分析 (1)根据勾股定理求得n的值;然后把点A的坐标代入函数解析式即可求得m的值;
(2)根据反比例函数图象的性质答题.
解答 解:(1)∵点A的坐标为(-2,n),OA=2$\sqrt{2}$.
∴4+n2=8,
则n=2或n=-2(舍去),
故点A的坐标为(-2,2),
又点A在反比例函数y=$\frac{m-3}{x}$的图象上,
∴m-3=-4,
则m=-1;
(2)由(1)易得反比例函数解析式是y=-$\frac{4}{x}$,
则该函数图象经过第二、四象限,且在每一象限内,y随x的增大而增大.
∵点C(a,y1),D(a+2,y2)(a>0),
∴a+2>a,
∴y1>y2.
点评 本题考查了反比例函数图象上点的坐标特征.解题时,需要熟悉反比例函数图象的性质.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.方程x2=4x的解是( )
| A. | x1=x2=4 | B. | x1=x2=0 | C. | x1=4,x2=0 | D. | x1=2,x2=-2 |
1.对于y=-2(x-3)2+2的图象下列叙述正确的是( )
| A. | 顶点作标为(-3,2) | B. | 对称轴为:直线x=-3 | ||
| C. | 当x≥3时y随x增大而减小 | D. | 函数的最小值是2 |
18.计算$\frac{1}{1×20}$+$\frac{1}{2×19}$+$\frac{1}{3×18}$+…+$\frac{1}{20×1}$-$\frac{20}{21}$($\frac{1}{1×19}$+$\frac{1}{2×18}$+…+$\frac{1}{19×1}$)的结果为( )
| A. | $\frac{1}{210}$ | B. | $\frac{1}{231}$ | C. | $\frac{1}{190}$ | D. | $\frac{1}{171}$ |
5.对于多项式a2+b2的意义解释不恰当的是( )
| A. | a,b两数的平方和 | |
| B. | 边长分别是a,b的两个正方形的面积 | |
| C. | 买a支单价a元的钢笔和买b支单价b元的铅笔的总价钱 |
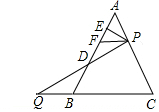 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC. 如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E.F分别为AC和AB的中点,则EF=3.
如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E.F分别为AC和AB的中点,则EF=3.