题目内容
20.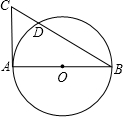 如图,已知AB是⊙O的直径,AC切⊙O于A,CB交⊙O于C,AC=2$\sqrt{6}$,CD=3,求⊙O的直径长.
如图,已知AB是⊙O的直径,AC切⊙O于A,CB交⊙O于C,AC=2$\sqrt{6}$,CD=3,求⊙O的直径长.
分析 连接AD,在Rt△ACD中可求得AD,再证明△ACD∽△BCA,利用相似三角形的性质可求得AB的长,即可求得⊙O的直径.
解答 解:
连接AD,
∵AB是直径,
∴∠ADB=90°,
∴在Rt△ADC中,AD=$\sqrt{A{C}^{2}-D{C}^{2}}$=$\sqrt{(2\sqrt{6})^{2}-{3}^{2}}$$\sqrt{15}$,
∵AC是⊙O的切线,
∴∠CAD=∠B,
∴△ACD∽△BCA,
∴$\frac{AD}{AB}$=$\frac{CD}{AC}$,即$\frac{\sqrt{15}}{AB}$=$\frac{3}{2\sqrt{6}}$,
解得AB=$\sqrt{40}$=2$\sqrt{10}$,即⊙O的直径长为2$\sqrt{10}$.
点评 本题主要考查切线的性质及相似三角形的判定和性质,由条件证得三角形相似是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 把1$\frac{1}{2}$,-2,π各数及它们的相反数在数轴上表示出来.并用“<”号连接.
把1$\frac{1}{2}$,-2,π各数及它们的相反数在数轴上表示出来.并用“<”号连接.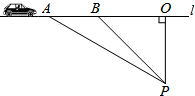 如图,已知测速站P到公路l的距离为40米,一辆汽车在公路l上行驶,测得从点A行驶到点B所用的时间为5秒,并测得∠APO=α,∠BPO=β,计算此车从A到B的平均速度为多少?(已知tanα=$\frac{12}{5}$,sinβ=$\frac{3}{5}$)
如图,已知测速站P到公路l的距离为40米,一辆汽车在公路l上行驶,测得从点A行驶到点B所用的时间为5秒,并测得∠APO=α,∠BPO=β,计算此车从A到B的平均速度为多少?(已知tanα=$\frac{12}{5}$,sinβ=$\frac{3}{5}$) 如图,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠2=∠BDE.
如图,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠2=∠BDE.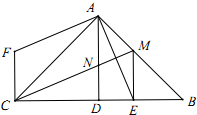 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足为D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.