题目内容
5.用配方法确定下列二次函数图象的对称轴和顶点坐标.(1)y=-$\frac{1}{2}$x2-2x+3;
(2)y=2(x-2)(x+3).
分析 (1)用配方法将抛物线的一般式转化为顶点式,可求顶点坐标和对称轴.
(2)化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解答 解:(1)y=-$\frac{1}{2}$x2-2x+3=y=-$\frac{1}{2}$(x+2)2+5,则对称轴是x=-2,顶点坐标是(-2,5);
(2)y=2(x-2)(x+3)=2(x-$\frac{1}{2}$)2-$\frac{25}{2}$.则对称轴是x=$\frac{1}{2}$,顶点坐标是($\frac{1}{2}$,-$\frac{25}{2}$).
点评 本题考查了二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
10.下列抛物线顶点坐标为(-2,3)的是( )
| A. | y=-2(x+2)2+3 | B. | y=-3(x-2)2+3 | C. | y=-5(x+2)2-3 | D. | y=-5(x-2)2-3 |
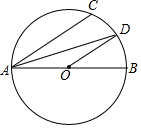 如图,AB为⊙O的直径,点C为半圆上一点,AD平分∠CAB交⊙O于点D
如图,AB为⊙O的直径,点C为半圆上一点,AD平分∠CAB交⊙O于点D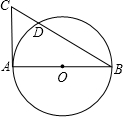 如图,已知AB是⊙O的直径,AC切⊙O于A,CB交⊙O于C,AC=2$\sqrt{6}$,CD=3,求⊙O的直径长.
如图,已知AB是⊙O的直径,AC切⊙O于A,CB交⊙O于C,AC=2$\sqrt{6}$,CD=3,求⊙O的直径长.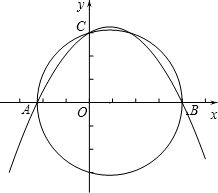 如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C)
如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C)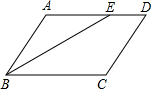 如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE.
如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE. 如图,在△ABC中,∠A=36°,∠ABC=∠ACB
如图,在△ABC中,∠A=36°,∠ABC=∠ACB