题目内容
20. 如图,在直角坐标系中,A(-1,0),B(0,2),一动点P沿过B点且垂直于AB的射线BM运动,P点的运动速度为每秒2个单位长度,射线BM与x轴交于点C.
如图,在直角坐标系中,A(-1,0),B(0,2),一动点P沿过B点且垂直于AB的射线BM运动,P点的运动速度为每秒2个单位长度,射线BM与x轴交于点C.(1)求点C的坐标;
(2)若P点开始运动时,Q点也同时开始从C出发,以每秒1个单位长度的速度沿x轴方向运动,t秒后,以P,Q,C为顶点的三角形为等腰三角形.求t的值.
分析 (1)先由A(-1,0),B(0,2),可得:OA=1,OB=2,然后根据射影定理可求出OC的值,进而确定点C的坐标;
(2)分三种情况讨论即可:①当PQ=QC时;②当PQ=PC时;③当PC=QC时.
解答 解:(1)∵A(-1,0),B(0,2),
∴OA=1,OB=2,
∵BC⊥AB,OB⊥AC,
∴OB2=OA•OC,
∴OC=4,
∴点C的坐标为:(4,0);
(2)∵点C的坐标为:(4,0),
∴OC=4,
∴AC=1+4=5,
在Rt△AOB中,由勾股定理得:
AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{5}$,
在Rt△BOC中,由勾股定理得:
BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=2$\sqrt{5}$,
∵P点的运动速度为每秒2个单位长度,Q点以每秒1个单位长度的速度沿x轴方向运动,
∴t秒后,BP=2t,CQ=t,
则PC=2$\sqrt{5}$-2t,
①当PQ=QC时,如图1,
作QE⊥PC,
∵PQ=QC,
∴EC=$\frac{1}{2}$PC=$\sqrt{5}$-t,
∵QE⊥BC,AB⊥BC,
∴QE∥AB,
∴△CEQ∽△CBA,
∴$\frac{CE}{BC}=\frac{CQ}{AC}$,
即$\frac{\sqrt{5}-t}{2\sqrt{5}}=\frac{t}{5}$,
解得:t=5$\sqrt{5}$-10;
②当PQ=PC时,如图2,
作PF⊥QC垂足为F,
∵PQ=PC,
∴FC=$\frac{1}{2}$QC=$\frac{1}{2}$t,
∵AB⊥BC,PF⊥QC,
∴∠ABC=∠PFC=90°,
∵∠PCF=∠ACP,
∴△PCF∽△ACB,
∴$\frac{PC}{AC}=\frac{FC}{BC}$,
即$\frac{2\sqrt{5}-2t}{5}=\frac{\frac{1}{2}t}{2\sqrt{5}}$,
解得:t=$\frac{64\sqrt{5}-40}{59}$;
③当PC=QC时,如图3,
∵PC=QC,
∴2$\sqrt{5}$-2t=t,
解得:t=$\frac{2\sqrt{5}}{3}$,
∴当t=5$\sqrt{5}$-10或t=$\frac{64\sqrt{5}-40}{59}$或t=$\frac{2\sqrt{5}}{3}$时,以P,Q,C为顶点的三角形为等腰三角形.
点评 此题是一次函数的综合题,主要考查了动点问题,等腰三角形的判定与性质,相似三角形的判定与性质等知识点,解(2)的关键是:分三种情况讨论:①当PQ=QC时;②当PQ=PC时;③当PC=QC时.

| 每公顷所需生产组/个 | 每公顷雨季产值 | |
| 蔬菜 | $\frac{1}{2}$ | 52500 |
| 水稻 | $\frac{1}{4}$ | 18000 |
| 篮球 | 排球 | |
| 进价(元/个) | 80 | 50 |
| 售价(元/个) | 95 | 60 |
(2)销售时,用6000元买了50个篮球和若干个排球,能获得利润多少?
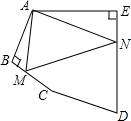 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC,DE上分别找出一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为多少?
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC,DE上分别找出一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为多少?