题目内容
5.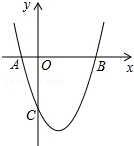 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.(1)求该抛物线的解析式;
(2)用配方法求该抛物线的对称轴以及顶点坐标;
(3)根据图象回答,当x为何值时,y>0,当x为何值时,y<0.
分析 (1)直接利用待定系数法求二次函数解析式得出答案;
(2)直接利用配方法求出二次函数对称轴和顶点坐标即可;
(3)利用A,B点坐标,再结合函数图象得出x的取值范围.
解答 解:(1)将A(-1,0),B(3,0)两点代入y=x2+bx+c得:
$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
故抛物线的解析式为:y=x2-2x-3;
(2)y=x2-2x-3
=(x-1)2-4,
故该抛物线的对称轴为直线x=1,顶点坐标为:(1,-4);
(3)如图所示:当x<-1或x>3时,y>0,当-1<x<3时,y<0.
点评 此题主要考查了抛物线与x轴的交点以及配方法求二次函数对称轴和顶点坐标以及利用函数图象判断不等式的解集等知识,正确利用数形结合得出x的取值范围是解题关键.

练习册系列答案
相关题目
6.已知3x=5,9y=10,则3x+2y=( )
| A. | 50 | B. | -100 | C. | 100 | D. | 无法确定 |
16.设O是等边三角形ABC内一点,已知∠AOB=130°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
| A. | 65° | B. | 60° | C. | 45° | D. | 70° |
10.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2-2b2,则( )
| A. | △ABC是直角三角形,且∠A为直角 | B. | △ABC是直角三角形,且∠B为直角 | ||
| C. | △ABC是直角三角形,且∠C为直角 | D. | △ABC不是直角三角形 |
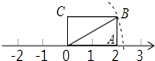 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是$±\sqrt{5}$.
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是$±\sqrt{5}$.