题目内容
14．
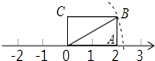如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交数轴于一点，则这个点表示的实数是$±\sqrt{5}$．
分析 根据勾股定理，可得OB的长，根据圆的性质，可得B点坐标．
解答 解：由勾股定理，得
OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{5}$．
B在原点的右侧时，B点表示的数为$\sqrt{5}$，
B在原点的左侧是，B点表示的数为-$\sqrt{5}$，
故答案为：$±\sqrt{5}$．
点评 本题考查了实数与数轴，利用勾股定理得出OB的长是解题关键，要分类讨论，以防遗漏．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
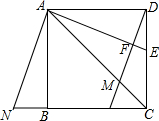已知正方形ABCD如图所示，连接其对角线AC，∠DAC的平分线AE交CD于点E，过点D作DM⊥AE于F，交AC于点M，共过点A作AN⊥AE交CB延长线于点N．
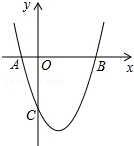如图，抛物线y=x2+bx+c与x轴交于A（-1，0），B（3，0）两点．
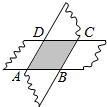如图，剪两张对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是平行四边形．
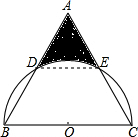如图，在边长为2的等边△ABC中，以BC为直径的半圆分别交AB、AC于点D、E，则图中阴影部分的面积是（结果保留π）$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$．
3．如图，反映的是某中学九（3）班学生外出方式（乘车、步行、骑车）的频数（人数）分布直方图（部分）和扇形分布图，那么下列说法正确的是（ ）
| A． | 九（3）班外出的学生共有42人 | |
| B． | 九（3）班外出步行的学生有8人 | |
| C． | 在扇形图中，步行的学生人数所占的圆心角为82 | |
| D． | 如果该校九年级外出的学生共有500人，那么估计全年级外出骑车的学生约有140人 |