Question

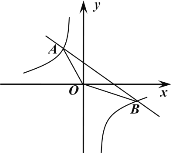
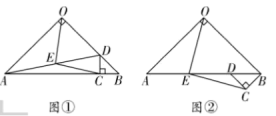
【题目】如图，在平面直角坐标系中，直线过点且与轴交于点．把点向左平移2个单位，再向上平移4个单位，得到点．过点的直线交轴于点．

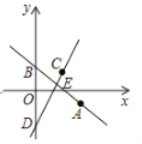
（1）求直线的解析式．

（2）直线与交于点，在直线和直线上是否存在点，使，若存在，求出点的坐标；若不存在，说明理由．

（3）若有过点的直线与线段有公共点且满足随的增大而减小，设直线与轴交点横坐标为，直接写出的取值范围________．

Answer 1

【答案】（1）；（2）存在，或；（3），

【解析】

（1）将代入直线求出其坐标后，根据点平移与坐标的变化求出点，代入直线即可得解.

（2）联立两直线解析式求出点坐标，进而求得的面积，令，即可解得到轴的距离，代入两直线解析式即可求得两个答案.

（3）有两种情况，第一种，由于直线满足随的增大而减小，根据一次函数的性质，可得，且直线过点，故；该直线与线段有公共点，其最大值即直线与轴的交点，解之即可.第二种最小值为直线与轴的交点，无上限，求得的解析式后令，解之即可.

（1）把代入得，则，

∵点向左平移2个单位，再向上平移4个单位，得到点，

∴．

将点代入， 得，解得，

∴直线的解析式为；

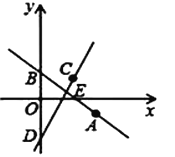
（2）令，

解得

∵

∴

把代入

把代入

综上，或

（3）第一种情况：

因为直线满足随的增大而减小，故，

直线过点，故直线与轴交点横坐标，

当直线过，时，与轴交点横坐标取最大值，

此时，

解得

所以直线解析式为，

令，解得，

故直线与轴交点横坐标取值范围为.

第二种情况：

当直线过，时，与轴交点横坐标取最小值，

此时

解得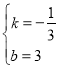

所以直线解析式为，

令，解得，

故直线与轴交点横坐标取值范围为.

综上，直线与轴交点横坐标取值范围为或.