Question

【题目】如图，为半圆的直径，点为半圆上任一点．

（1）若，过点作半圆的切线交直线于点．求证：；

（2）若，过点作的平行线交半圆于点．当以点，，，为顶点的四边形为菱形时，求的长．

Answer 1

【答案】（1）证明见解析；（2）或．

【解析】

（1）由圆周角定理得到∠ACB=90°，先证△OＡC是等边三角形，根据等边三角形和外角的性质得到∠OAP=∠BOC=120°，根据切线的性质得到∠OCP=90°,进一步得到∠ACP=∠OCB，最后根据全等三角形的判定定理证明即可；

（2）根据菱形的性质得到OA=AD=CD=OC，连接OD，得到△AOD与△COD是等边三角形，根据等边三角形的性质得到∠AOD=∠COD=60°，求得∠BOC=60°，根据弧长公式即可得到结论

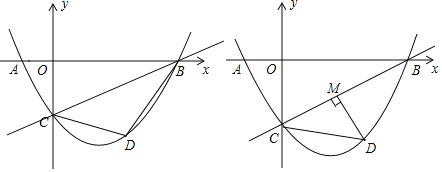
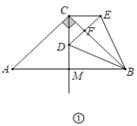
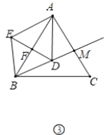
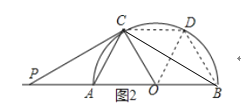
解： （1）如图2∵AB为直径，

∴∠ACB=90°，

∴∠BAC=60°，

∴∠ABC=30°

∴AC=AB=OA=OB=OC

∴△OAC是等边三角形

∴OC=AC，∠OAC=∠AOC=60°

∴∠CAP=∠BOC=120°

∴CP是⊙O的切线，

∴ OC⊥PC，

∴∠OCP=90°

∴∠ACP=∠OCB，

在△PBC与△AOC中，

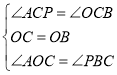
∴(ASA)

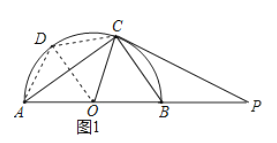
(2)如图1，连接OD,BD,CD

∵四边形AOCD是菱形

∴OA=AD=CD=OC，OA=OD=OC

∴△AOD与△COD是等边三角形，

∵.∠AOD=∠COD=60°，

∴∠BOC=60°，

∴

同理:如图2可得:

故的长度为或．