题目内容
4.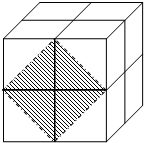 如图,这是由8个同样大小的立方体组成的魔方,体积为64cm3.
如图,这是由8个同样大小的立方体组成的魔方,体积为64cm3.(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形,求出阴影部分的面积及其边长.
分析 (1)立方体的体积等于棱长的3次方,开立方即可得出棱长;
(2)根据魔方的棱长为4,所以小立方体的棱长为2,阴影部分由4个直角三角形组成,算出一个直角三角形的面积乘以4即可得到阴影部分的面积,开平方即可求出边长.
解答 解:(1)$\root{3}{64}=4$(cm).
(2)∵魔方的棱长为4cm,
∴小立方体的棱长为2cm,
∴阴影部分面积为:$\frac{1}{2}$×2×2×4=8(cm2),
边长为:$\sqrt{8}$=$2\sqrt{2}$(cm).
点评 本题考查的是立方根在实际生活中的运用,解答此题的关键是根据立方根求出魔方的棱长.

练习册系列答案
相关题目
9.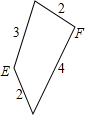 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )| A. | $\frac{4}{3}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{3}$或$\frac{24}{5}$ | D. | $\frac{2}{3}$或$\frac{12}{5}$ |
16.某课外学习小组有5人,在一次数学测验中的成绩分别是120、130、135、120、125,下列说法不正确的是( )
| A. | 众数是120 | B. | 方差是34 | C. | 中位数是135 | D. | 平均数是126 |
13.学校组织的实践活动中,晓华同学用纸板制作了一个圆锥模型,它的底面直径为4,高为2$\sqrt{3}$,则这个圆锥的侧面积是( )
| A. | 8π | B. | 16π | C. | 4$\sqrt{3}$π | D. | 8$\sqrt{7}$π |
14.下列结论正确的是( )
| A. | $-\sqrt{(-6)^{2}}=-6$ | B. | $(-\sqrt{3})^{2}=9$ | C. | $\sqrt{({-16)}^{2}}=±16$ | D. | $-(-\sqrt{\frac{16}{25}})^{2}=\frac{16}{25}$ |
 如图,一次函数y=x+6的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为36.
如图,一次函数y=x+6的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为36.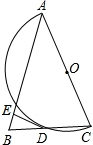 如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E
如图,在△ABC中,AB=AC,以AC为直径的半圆O与边BC相交于点D,DE⊥AB,垂足为E