题目内容
7. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=52°,则∠2=104°.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=52°,则∠2=104°.
分析 由折叠的性质可得:∠DEF=∠GEF,根据平行线的性质:两直线平行,内错角相等可得:∠DEF=∠EFG=55°,从而得到∠GEF=55°,根据平角的定义即可求得∠1,再由平行线的性质求得∠2.
解答 解:∵AD∥BC,∠EFG=52°,
∴∠DEF=∠EFG=52°(两直线平行,内错角相等),
∠1+∠2=180°(两直线平行,同旁内角互补),
由折叠的性质可得:∠GEF=∠DEF=52°,
∴∠1=180°-∠GEF-∠DEF=180°-52°-52°=76°,
∴∠2=180°-∠1=104°.
故答案为:104°.
点评 此题主要考查折叠的性质,平行线的性质和平角的定义,解决问题的关键是根据折叠的方法找准对应角,求出∠GEF的度数.

练习册系列答案
相关题目
12.在平面直角坐标系中,下面的点在第四象限的是( )
| A. | (7,-1) | B. | (0,-3) | C. | (-2,-3) | D. | (1,3) |
19.下列各数中,不是无理数的是( )
| A. | $\sqrt{7}$ | B. | $\root{3}{125}$ | ||
| C. | π | D. | 0.15115111511115… |
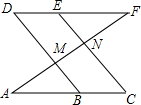 如图,已知DF∥AC,∠C=∠D,求证:∠AMB=∠ANC.
如图,已知DF∥AC,∠C=∠D,求证:∠AMB=∠ANC.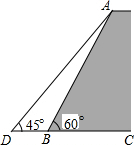 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)