题目内容
14.已知3x-2y=0.求:(1)$\frac{x}{y}$; (2)$\frac{x+y}{y}$; (3)$\frac{x+2}{y+3}$.
分析 由已知条件得到3x=2y,根据内项之积等于外项之积得到$\frac{x}{y}$=$\frac{2}{3}$;根据合比性质可得$\frac{x+y}{y}$的值,根据等比性质可得$\frac{x+2}{y+3}$的值.
解答 解:∵3x-2y=0,
∴3x=2y,
(1)$\frac{x}{y}$=$\frac{2}{3}$;
(2)$\frac{x+y}{y}$=$\frac{2+3}{3}$=$\frac{5}{3}$;
(3)$\frac{x+2}{y+3}$=$\frac{x}{y}$=$\frac{2}{3}$.
点评 本题考查了比例的性质:常用的性质有:内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.

练习册系列答案
相关题目
5.下列方程中一定是一元二次方程的是( )
| A. | x2=0 | B. | x+$\frac{1}{3-x}$-2x2=0 | C. | ax2+bx+c=0 | D. | x2+2y+3=0 |
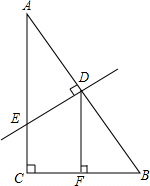 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB、AC于点D、E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB、AC于点D、E. 如图所示,∠BAC=85°,BF平分∠ABC交AC于点F,∠BFC=100°,求∠C的度数.
如图所示,∠BAC=85°,BF平分∠ABC交AC于点F,∠BFC=100°,求∠C的度数.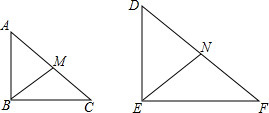 如图,Rt△ABC∽Rt△DEF,且DE=2AB,BM,EN是斜边上的中线
如图,Rt△ABC∽Rt△DEF,且DE=2AB,BM,EN是斜边上的中线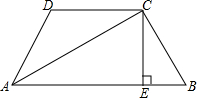 如图,已知在四边形ABCD中.∠B+∠D=180°,AC平分∠BAD,CE⊥AB,E为垂足.求证:AB+AD=2AE.
如图,已知在四边形ABCD中.∠B+∠D=180°,AC平分∠BAD,CE⊥AB,E为垂足.求证:AB+AD=2AE.