题目内容
16.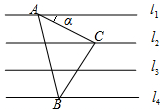 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果等腰Rt△ABC(∠ACB=90°)的三个顶点分别在三条直线上,则sinα=$\frac{\sqrt{5}}{5}$.
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果等腰Rt△ABC(∠ACB=90°)的三个顶点分别在三条直线上,则sinα=$\frac{\sqrt{5}}{5}$.
分析 过C作EF⊥l1,垂足为E,交l4于点F,由条件可证明△BFC≌△CEA,则可求得AE=2CE,在Rt△AEC中可求得AC,可求得答案.
解答 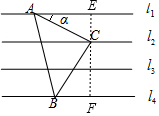 解:
解:
如图,过C作EF⊥l1,垂足为E,交l4于点F,
由题意可知AC=BC,∠ACB=90°,
∴∠BCF+∠ACE=∠EAC+∠ACE=90°,
∴∠EAC=∠BCF,
在△BFC和△CEA中
$\left\{\begin{array}{l}{∠BCF=∠CAE}\\{∠BFC=∠CEA}\\{BC=AC}\end{array}\right.$
∴△BFC≌△CEA(AAS),
∴AE=CF,
又CF=2CE,
∴AE=2EC,
在Rt△ACE中,由勾股定理可知AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{5}$CE,
∴sinα=$\frac{CE}{AC}$=$\frac{CE}{\sqrt{5}CE}$=$\frac{\sqrt{5}}{5}$,
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题主要考查全等三角形的判定和性质及三角函数的定义,由条件构造三角形全等,求得AC与CE的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 已知:如图,∠AOB=40°,点P为∠AOB内一点,P′,P″分别是点P关于OA、OB的对称点,连接P′P″,分别交OA于M、OB于N.如果P′P″=5cm,△PMN的周长为l,∠P′OP′′的度数为α,请根据以上信息完成作图,并指出l和α的值.( )
已知:如图,∠AOB=40°,点P为∠AOB内一点,P′,P″分别是点P关于OA、OB的对称点,连接P′P″,分别交OA于M、OB于N.如果P′P″=5cm,△PMN的周长为l,∠P′OP′′的度数为α,请根据以上信息完成作图,并指出l和α的值.( )
 已知:如图,∠AOB=40°,点P为∠AOB内一点,P′,P″分别是点P关于OA、OB的对称点,连接P′P″,分别交OA于M、OB于N.如果P′P″=5cm,△PMN的周长为l,∠P′OP′′的度数为α,请根据以上信息完成作图,并指出l和α的值.( )
已知:如图,∠AOB=40°,点P为∠AOB内一点,P′,P″分别是点P关于OA、OB的对称点,连接P′P″,分别交OA于M、OB于N.如果P′P″=5cm,△PMN的周长为l,∠P′OP′′的度数为α,请根据以上信息完成作图,并指出l和α的值.( )| A. | l=5cm,α=80° | B. | l=5cm,α=85° | C. | l=6cm,α=80° | D. | l=6cm,α=85° |
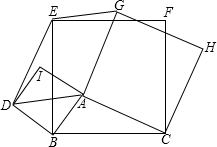 如图以△ABC的各边,在边BC的同侧分别作三个正方形,它们分别是正方形ABDI,BCFE,ACHG,则四边形ADEG的形状为平行四边形.
如图以△ABC的各边,在边BC的同侧分别作三个正方形,它们分别是正方形ABDI,BCFE,ACHG,则四边形ADEG的形状为平行四边形.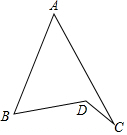 已知如图所示,∠B=60°,∠C=20°,∠BDC=3∠A,求∠A的度数.
已知如图所示,∠B=60°,∠C=20°,∠BDC=3∠A,求∠A的度数.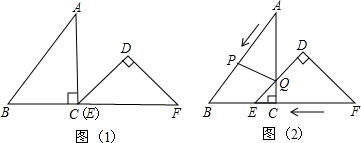
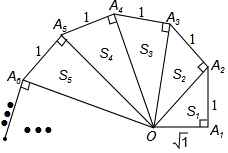 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题.