题目内容
6. 已知:如图,∠AOB=40°,点P为∠AOB内一点,P′,P″分别是点P关于OA、OB的对称点,连接P′P″,分别交OA于M、OB于N.如果P′P″=5cm,△PMN的周长为l,∠P′OP′′的度数为α,请根据以上信息完成作图,并指出l和α的值.( )
已知:如图,∠AOB=40°,点P为∠AOB内一点,P′,P″分别是点P关于OA、OB的对称点,连接P′P″,分别交OA于M、OB于N.如果P′P″=5cm,△PMN的周长为l,∠P′OP′′的度数为α,请根据以上信息完成作图,并指出l和α的值.( )| A. | l=5cm,α=80° | B. | l=5cm,α=85° | C. | l=6cm,α=80° | D. | l=6cm,α=85° |
分析 连接OP,由对称的性质得:OA、OB分别是PP′和PP″的中垂线,由中垂线的性质得:PM=P′M,PN=P′N,P′O=PO,PO=P″O,再根据等腰三角形三线合一的性质求出α的度数,同时求出l的长.
解答  解:连接OP,
解:连接OP,
∵P与P′关于OA对称,
∴OA是PP′的中垂线,
∴P′M=PM,P′O=PO,
同理得:PN=P″N,PO=P″O,
∴∠P′OA=∠POA,∠P″OB=∠POB,
∵∠P′OP″=α=2∠AOB=2×40°=80°,
∵△PMN的周长=l=PM+PN+MN=P′M+P′N+MN=P′P″=5cm;
故选A.
点评 本题考查了轴对称的性质、中垂线的性质、等腰三角形三线合一的性质,明确对称轴是对称点连线的中垂线是关键,并熟练掌握等腰三角形三线合一的性质,这在等腰三角形中经常运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.将面积为a2的正方形边长增加3,则正方形的面积增加了( )
| A. | 9 | B. | 2a+9 | C. | 3a+9 | D. | 6a+9 |
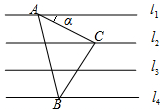 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果等腰Rt△ABC(∠ACB=90°)的三个顶点分别在三条直线上,则sinα=$\frac{\sqrt{5}}{5}$.
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果等腰Rt△ABC(∠ACB=90°)的三个顶点分别在三条直线上,则sinα=$\frac{\sqrt{5}}{5}$. 已知在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm.求证:AB=AC.
已知在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm.求证:AB=AC. 如图,AB和CD交于点O,AO=2,OD=3,OC=4,OB=6,求证:∠A=∠D.
如图,AB和CD交于点O,AO=2,OD=3,OC=4,OB=6,求证:∠A=∠D. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
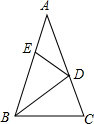 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )