题目内容
19.如图,已知线段AB长为6,点A在x轴负半轴,B在y轴正半轴,绕A点顺时针旋转60°,B点恰好落在x轴上D点处,点C在第一象限内且四边形ABCD是平行四边形.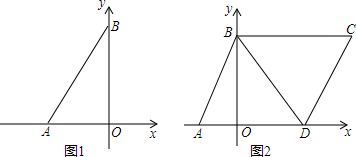
(1)求点C、点D的坐标;
(2)若半径为1的⊙P从点A出发,沿A-B-D-C以每秒4个单位长的速度匀速移动,同时⊙P的半径以每秒0.4个单位长的速度增加,运动到点C时运动停止,当运动时间为t秒时,①t为何值时,⊙P与y轴相切?
②在运动过程中,是否存在一个时刻,⊙P与四边形ABCD四边都相切?若存在,说出理由;若不存在,问题中⊙P的半径以每秒0.4个单位长速度增加改为多少时就存在.
(3)若线段AB绕点O顺时针旋转180°,线段AB扫过的面积是多少.
分析 (1)求出OB的长得出点C的坐标,求出AD的长即可求出点D的坐标,
(2)①分两种情况讨论:当P在AB上时,若⊙P与y轴相切,则1+0.5t=3-2t,当P在BD上时,若⊙P与y轴相切,则1+0.5t=2t-3,再求解即可,
②设⊙P的半径以acm/s的速度增加,当点P在菱形ABCD的对角线交点时,与四边形ABCD都相切,⊙P的半径1+$\frac{9}{4}$a,再求出BD和AC的交点坐标,最后根据若⊙P与四边形ABCD相切,则1+$\frac{9}{4}$a=1.5$\sqrt{3}$,即可得出答案,
(3)过O作OE⊥AB,根据△BOA∽△OEA,求出OE,从而求出S=$\frac{1}{2}$[(3$\sqrt{3}$)2π-(1.5$\sqrt{3}$)2π],再计算即可.
解答 解(1)∵OB=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴点C的坐标是(6,3$\sqrt{3}$),
∵AD=AB=6,
∴点D的坐标是(3,0),
(2)①当P在AB上时,若⊙P与y轴相切,则1+0.5t=3-2t,
t=$\frac{4}{5}$,
当P在BD上时,若⊙P与y轴相切,则1+0.5t=2t-3,
t=$\frac{8}{3}$,
②不存在
设⊙P的半径以acm/s的速度增加,
当点P在菱形ABCD的对角线交点时,到ABCD的距离相等,即与四边形ABCD都相切,
此时t=$\frac{9}{4}$,⊙P的半径1+$\frac{9}{4}$a,
设BD的解析式为:y=kx+b,AC的解析式为:y=ax+c,
解得:BD的解析式为:y=-$\sqrt{3}$x+3$\sqrt{3}$,AC的解析式为:y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
-$\sqrt{3}$x+3$\sqrt{3}$=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
解得;x=$\frac{3}{2}$,
则y=1.5$\sqrt{3}$,
若⊙P与四边形ABCD相切,
则1+$\frac{9}{4}$a=1.5$\sqrt{3}$,
解得:a=$\frac{6\sqrt{3}-4}{9}$,
则⊙P的半径以$\frac{6\sqrt{3}-4}{9}$cm/s的速度运动时就存在,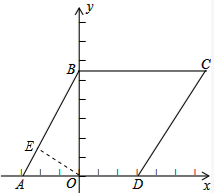
(3)过O作OE⊥AB,
则△BOA∽△OEA,
$\frac{BO}{OE}$=$\frac{BA}{OA}$,
解得;OE=1.5$\sqrt{3}$,
S=$\frac{1}{2}$[(3$\sqrt{3}$)2π-(1.5$\sqrt{3}$)2π]=$\frac{81}{8}$π,
则线段AB扫过的面积是$\frac{81}{8}$π.
点评 此题考查了圆的综合,用到的知识点是菱形的性质、切线的判定、相似三角形的判定与性质、一次函数,关键是作出辅助线构造相似三角形,注意分类讨论.

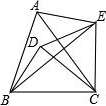 如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )
如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )| A. | 30 | B. | 40 | C. | 45 | D. | 60 |

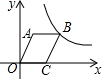 如图,在平行四边形OABC中,OC=3,OA=4,∠AOC=60°,若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,则k的值为10$\sqrt{3}$.
如图,在平行四边形OABC中,OC=3,OA=4,∠AOC=60°,若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,则k的值为10$\sqrt{3}$. 如图,已知锐角△ABC.
如图,已知锐角△ABC.