题目内容
12.已知抛物线y=-$\frac{1}{2}$x2-x+4(1)通过配方,写出它的顶点坐标,并求出它与x轴的交点坐标.
(2)若点A(m,y1),B(n,y2)(m<n<-1)都在该抛物线上,则y1<y2(填>、<或=)
分析 (1)直接利用配方法求出二次函数对称轴顶点坐标,再利用y=0求出x的值,即可得出它与x轴的交点坐标;
(2)利用二次函数增减性,即可得出对应y的大小关系.
解答 解:(1)y=-$\frac{1}{2}$x2-x+4
=-$\frac{1}{2}$(x2+2x)+4
=-$\frac{1}{2}$(x+1)2+$\frac{9}{2}$,
故顶点坐标为:(-1,$\frac{9}{2}$),
当y=0,则0=-$\frac{1}{2}$(x+1)2+$\frac{9}{2}$,
解得:x1=2,x2=-4,
即它与x轴的交点坐标为:(2,0),(-4,0);
(2)∵y=-$\frac{1}{2}$(x+1)2+$\frac{9}{2}$的对称轴为:x=-1,且m<n<-1,
∴A,B点都在对称轴左侧,
∵抛物线开口向下,
∴抛物线对称轴左侧,y随x的增大而增大,
∴y1<y2.
故答案为:<.
点评 此题主要考查了配方法求二次函数顶点坐标以及二次函数增减性,正确掌握函数顶点坐标求法是解题关键.

练习册系列答案
相关题目
7.某品牌汽车4s店经销的一款汽车分为电动版和燃油版两种,电动版汽车行驶每千米耗电折合0.15元,燃油版汽车行驶每千米耗油折合0.65元,该4s店一月份和二月份的销售记录如下:
(1)求该款汽车的电动版汽车和燃油版汽车每辆的售价分别是多少?
(2)若两种车的预计使用寿命都为10年,某购车家庭平均每月行驶x千米,每年还需负担占购车价值10%的保养、保险等各项费用.请根据家庭平均每月行驶千米数x分析,购买使用哪种车型较为经济?(仅考虑购车款、油电消耗,占购车价值10%的保养、保险等各项费用)
| 月份 | 燃油版 | 电动版 | 销售收入 |
| 一月 | 10辆 | 2辆 | 165万元 |
| 二月 | 12辆 | 1辆 | 170万元 |
(2)若两种车的预计使用寿命都为10年,某购车家庭平均每月行驶x千米,每年还需负担占购车价值10%的保养、保险等各项费用.请根据家庭平均每月行驶千米数x分析,购买使用哪种车型较为经济?(仅考虑购车款、油电消耗,占购车价值10%的保养、保险等各项费用)
17.下列运算正确的是( )
| A. | -$\frac{5}{7}$+$\frac{2}{7}$=-($\frac{5}{7}$+$\frac{2}{7}$)=-1 | B. | -7-2×5=-9×5=-45 | ||
| C. | 3÷$\frac{5}{4}$×$\frac{4}{5}$=3÷1=3 | D. | |3-5|=-(3-5) |

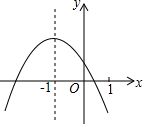 如图是抛物线y=ax2+bx+c的图象,则下列说法正确的有( )个.
如图是抛物线y=ax2+bx+c的图象,则下列说法正确的有( )个.