题目内容
5.若一个正整数,它的各位数字是左右对称的,则称这个数是对称数,如22,797,12021都是对称数,最小的对称数是11,没有最大的对称数,因为数位是无穷的.(1)若将任意一个各位数字均不为零的四位对称数分解为前两位数所表示的数和后两位数所表示的数,请你证明这两个数的和一定能被11整除;
(2)若将一个三位对称数$\overline{aba}$加上其各位数字之和(其中0<a≤9,0≤b≤9),所得的结果能被13整除,求所有满足条件的三位对称数.
分析 (1)若四位数abba是一个各位数字均不为零的四位对称数,它分解为两位数所表示的数和后两位数所表示的数为(10a+b)与(10b+a),则(10a+b)+10b+a=11a+11b=11(a+b),由此即可证明.
(2)三位对称数$\overline{aba}$加上其各位数字之和为100a+10b+a+2a+b=103a+11b,由0<a≤9,0≤b≤9,且103a+11b是13的倍数,用例举法即可解决问题.
解答 解:(1)若四位数abba是一个各位数字均不为零的四位对称数,
它分解为两位数所表示的数和后两位数所表示的数为(10a+b)与(10b+a),
所以(10a+b)+10b+a=11a+11b=11(a+b)
由于a、b均是整数,
所以分解后的两数的和一定能被11整除;
(2)三位对称数$\overline{aba}$加上其各位数字之和为100a+10b+a+2a+b=103a+11b,
∵0<a≤9,0≤b≤9,且103a+11b是13的倍数,
可得$\left\{\begin{array}{l}{a=1}\\{b=6}\end{array}\right.$或$\left\{\begin{array}{l}{a=3}\\{b=5}\end{array}\right.$或$\left\{\begin{array}{l}{a=5}\\{b=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=7}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=8}\\{b=9}\end{array}\right.$或$\left\{\begin{array}{l}{a=9}\\{b=2}\end{array}\right.$,
∴满足条件的三位数是161或353或545或737或898或929.
点评 本题考查因式分解的应用,数字问题等知识,解题的关键是理解题意,学会用代数式解决问题,学会用例举法解决问题,属于中考常考题型.

| A. | (-2,3) | B. | (2,3) | C. | (-2,-3) | D. | (2,-3) |
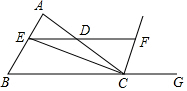 如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.
如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.