题目内容
已知x、y、z都不小于0,且满足3y+2z=3-x及3y+z=4-3x,求函数u=3x-2y+4z的最大值与最小值.
考点:函数最值问题
专题:计算题
分析:解关于y与z的方程组
,得z=2x-1,y=-
x+
,再利用x、y、z都不小于0得到
,解不等式组可确定x的取值范围
≤x≤1,
然后把z=2x-1,y=-
x+
代入u=3x-2y+4z得到关于u与x的一次函数关系u=
x-
(
≤x≤1),再利用一次函数的性质确定u的最大和最小值.
|
| 5 |
| 3 |
| 5 |
| 3 |
|
| 1 |
| 2 |
然后把z=2x-1,y=-
| 5 |
| 3 |
| 5 |
| 3 |
| 43 |
| 3 |
| 22 |
| 3 |
| 1 |
| 2 |
解答:解:
,
①-②得z=2x-1③,
把③代入②得3y+2x-1=4-3x,
所以y=-
x+
,
∵x、y、z都不小于0,
∴
,解得
≤x≤1,
∵u=3x-2y+4z=3x-2(-
x+
)+4(2x-1)
=
x-
,
∴当x=
时,u的值最小,最小值=
×
-
=-
;
当x=1时,u的值最大,最大值=
-
=7,
即函数u=3x-2y+4z的最大值与最小值分别为7,-
.
|
①-②得z=2x-1③,
把③代入②得3y+2x-1=4-3x,
所以y=-
| 5 |
| 3 |
| 5 |
| 3 |
∵x、y、z都不小于0,
∴
|
| 1 |
| 2 |
∵u=3x-2y+4z=3x-2(-
| 5 |
| 3 |
| 5 |
| 3 |
=
| 43 |
| 3 |
| 22 |
| 3 |
∴当x=
| 1 |
| 2 |
| 43 |
| 3 |
| 1 |
| 2 |
| 22 |
| 3 |
| 1 |
| 6 |
当x=1时,u的值最大,最大值=
| 43 |
| 3 |
| 22 |
| 3 |
即函数u=3x-2y+4z的最大值与最小值分别为7,-
| 1 |
| 6 |
点评:本题考查了函数最值问题:熟练掌握一次函数y=kx+b(k≠0,k,b为常数)的性质(当k>0,图象经过第一,三象限,y随x的增大而增大;当k<0,图象经过第二,四象限,y随x的增大而减小).

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
下列运算中正确的是( )
| A、a2•a3=a5 |
| B、(ab)2=a2b |
| C、(a3)2=a5 |
| D、a6÷a2=a3 |
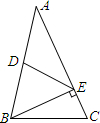 如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=5,AE=8,则BE的长度是( )
如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=5,AE=8,则BE的长度是( )| A、5 | B、5.5 | C、6 | D、6.5 |
 如图,直线l上摆有三个正方形a,b,c,若a、c的面积分别为10和8,则b的面积是( )
如图,直线l上摆有三个正方形a,b,c,若a、c的面积分别为10和8,则b的面积是( )| A、16 | B、20 | C、18 | D、24 |