题目内容
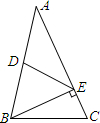如图，△ABC中，D为AB中点，E在AC上，且BE⊥AC．若DE=5，AE=8，则BE的长度是（ ）| A、5 | B、5.5 | C、6 | D、6.5 |
考点：勾股定理,直角三角形斜边上的中线
专题：
分析：根据直角三角形斜边上的中线求出AB长，根据勾股定理求出BE即可．
解答：解：∵BE⊥AC，
∴∠BEA=90°，
∵DE=5，D为AB中点，
∴AB=2DE=10，
∵AE=8，
∴由勾股定理得：BE=
=6，
故选C．
∴∠BEA=90°，
∵DE=5，D为AB中点，
∴AB=2DE=10，
∵AE=8，
∴由勾股定理得：BE=
| AB2-AE2 |
故选C．
点评：本题考查了直角三角形斜边上的中线和勾股定理的应用，注意：在直角三角形中，两直角边的平方和等于斜边的平方．
练习册系列答案
相关题目
已知一次函数中，y=（m+2）x-1的值随着x的增大而增大，则m的取值范围是（ ）
| A、m＞0 | B、m＜0 |
| C、m＞-2 | D、m＜-2 |
如图，P是∠α的边OA上一点，且点P的坐标为（3，4），则tanα的值是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
若∠α与∠β互为补角，且∠α是∠β的3倍，则∠β为（ ）
| A、45° | B、60° |
| C、90° | D、135° |
下列命题的逆命题正确的是（ ）
| A、全等三角形的面积相等 |
| B、全等三角形的周长相等 |
| C、等腰三角形的两个底角相等 |
| D、直角都相等 |
如图，晚上小亮在路灯下散步，在从A处走向B处的过程中，他在地上的影子（ ）| A、逐渐变短 |
| B、先变短后再变长 |
| C、逐渐变长 |
| D、先变长后再变短 |
给出四个数：0，
，-2，3.14，其中最小的是（ ）
| 7 |
| A、0 | ||
B、
| ||
| C、-2 | ||
| D、3.14 |