题目内容
15.不等式组$\left\{\begin{array}{l}{\frac{1}{2}x-1≤7-\frac{3}{2}x}\\{5x+2>3(x-1)}\end{array}\right.$的所有整数解的和是m,则m的算术平方根在哪两个相邻的整数之间( )| A. | 2,3 | B. | 3,4 | C. | 1,2 | D. | 0,1 |
分析 先求出不等式组的解集,再求出不等式组的整数解,求出m和m的算术平方根,即可得出选项.
解答 解:$\left\{\begin{array}{l}{\frac{1}{2}x-1≤7-\frac{3}{2}x①}\\{5x+2>3(x-1)②}\end{array}\right.$
∵解不等式①得:x≤4,
解不等式②得:x>-2.5,
∴不等式组的解集为-2.5<x≤4,
∴不等式组的整数解为-2,-1,0,1,2,3,4,
∴m=(-2)+(-1)+0+1+2+3+4=7,
∵2<$\sqrt{7}$<3,
∴m的算术平方根在2和3之间,
故选A.
点评 本题考查了一元一次不等式组的整数解,算术平方根,估算无理数的大小等知识点,能求出m的值是解此题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
5.下列运算正确的是( )
| A. | a3•a2=a5 | B. | a6÷a2=a3 | C. | (a2)2=a6 | D. | (3a)3=3a3 |
6.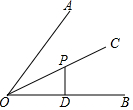 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
10.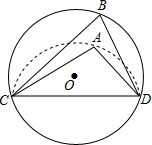 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )| A. | 110° | B. | 70° | C. | 60° | D. | 55° |
20.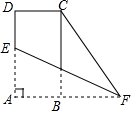 如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
 如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
4.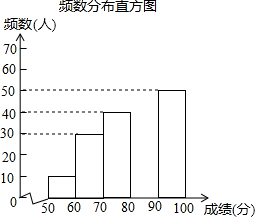 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
根据所给信息,解答下列问题:
(1)m=70,n=0.2;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:频数频率分布表
| 成绩x(分) | 频数(人) | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
(1)m=70,n=0.2;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
5.关于x的一元二次方程x2-2x+k=0有两个相等的实数根,则k的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.
如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.