题目内容
6.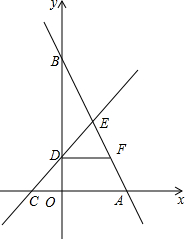 如图,直线y=kx+b分别与x轴、y轴交于点A(2,0)和点B,直线y=x+1分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为CE的中点.
如图,直线y=kx+b分别与x轴、y轴交于点A(2,0)和点B,直线y=x+1分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为CE的中点.(1)求直线y=kx+b的解析式;
(2)过点D作DF∥x轴,交直线y=kx+b于点F,则△DEF的面积为$\frac{3}{4}$.
分析 (1)过E作EH⊥y轴于H,由y=x+1,求得D的坐标为(0,1)C(-1,0),再证得△COD≌△EHD,根据全等三角形的判定得到EH=OC=1,DH=OD=1,即可求得E点的坐标由待定系数法即可求得直线y=kx+b的解析式;
(2)根据三角形的中位线定理求得DE,由E(1,2),D的坐标为(0,1),求得E到DF的距离为,根据三角形的面积公式即可求得结论.
解答 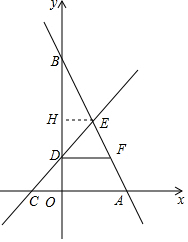 解:(1)过E作EH⊥y轴于H
解:(1)过E作EH⊥y轴于H
把x=0代入y=x+1,得y=1,
∴D的坐标为(0,1),
∴OD=1,
把y=0代入y=x+1,得x=-1,
∴C(-1,0),
∵点D为CE的中点,
∴△COD≌△EHD,
∴EH=OC=1,DH=OD=1,
∴E(1,2),把A,E点的坐标代入y=kx+b中,得$\left\{\begin{array}{l}{2k+b=0}\\{k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
∴直线y=kx+b的解析式为y=-2x+4;
(2)把y=0代入y=-2x+4,得x=2,
∴A(2,0),
∴AC=3,
∵D为CE的中点,DF∥x轴,
∴F为EA的中点,
∴DE=$\frac{1}{2}$AC=$\frac{3}{2}$,
∵E(1,2),D的坐标为(0,1),
∴E到DF的距离为1,
∴△DEF的面积=$\frac{1}{2}$×$\frac{3}{2}$×1=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题主要考查了直线与坐标轴的交点坐标的求法,三角形全等的性质和判定,待定系数法求一次函数的解析式,通过全等三角形求得E点的坐标是解题的关键.

 发散思维新课堂系列答案
发散思维新课堂系列答案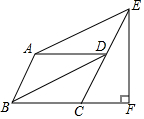 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
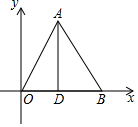 如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.
如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.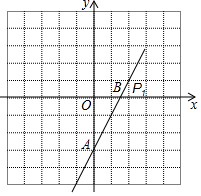 如图,直线l:y=mx-3与x轴、y轴分别交于点A、B,点P1(2,1)在直线l上,将点P1先向右平移1个单位,再向上平移2个单位得到像点P2.
如图,直线l:y=mx-3与x轴、y轴分别交于点A、B,点P1(2,1)在直线l上,将点P1先向右平移1个单位,再向上平移2个单位得到像点P2.