题目内容
14.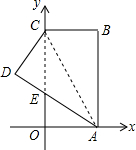 如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是( )
如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是( )| A. | (-$\frac{3}{5}$,$\frac{8}{3}$) | B. | (-$\frac{3}{5}$,2) | C. | (-$\frac{4}{5}$,$\frac{14}{5}$) | D. | (-$\frac{4}{5}$,$\frac{12}{5}$) |
分析 过D作DF⊥AF于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=1,设OE=m,那么CE=3-m,DE=m,利用勾股定理即可求出m,然后利用已知条件可以证明△AEO∽△ADF,而AD=AB=3,接着利用相似三角形的性质即可求出DF、AF的长度,也就求出了点D的坐标.
解答 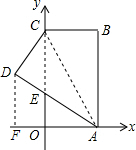 解:如图,过D作DF⊥AO于F,
解:如图,过D作DF⊥AO于F,
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,
设OE=m,那么CE=3-m,DE=m,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(3-m)2=m2+12,
解得m=$\frac{4}{3}$,
∵DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
而AD=AB=3,
∴AE=CE=3-$\frac{4}{3}$=$\frac{5}{3}$,
∴$\frac{AE}{AD}$=$\frac{EO}{DF}$=$\frac{AO}{AF}$,
即$\frac{\frac{5}{3}}{3}=\frac{\frac{4}{3}}{DF}$=$\frac{AO}{AF}$,
∴DF=$\frac{12}{5}$,AF=$\frac{9}{5}$,
∴OF=$\frac{9}{5}$-1=$\frac{4}{5}$,
∴D的坐标为(-$\frac{4}{5}$,$\frac{12}{5}$).
故选D.
点评 此题主要考查了图形的折叠问题,也考查了坐标与图形的性质,解题的关键是把握折叠的隐含条件,利用隐含条件得到全等三角形和相似三角形,然后利用它们的性质即可解决问题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
6.一学生扔实心球,实心球行进的高度y(m)与水平距离x(m)的函数表达式为y=-$\frac{1}{5}$x2+$\frac{7}{5}$x+$\frac{8}{5}$,则实心球落地时的水平距离是( )
| A. | 1m | B. | 8m | C. | 9m | D. | 10m |
3.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
则抛物线的对称轴是x=$\frac{1}{2}$.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
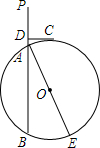 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上的一点,且AC平分∠PAE,过C作CD⊥PA于点D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上的一点,且AC平分∠PAE,过C作CD⊥PA于点D.