��Ŀ����
6����ͼ���ڡ�ABC�У�AB=AC��AD��BC�ڵ�D��BC=10cm��AD=8cm����P�ӵ�B���������߶�BC����ÿ��3cm���ٶ����C�����˶������ͬʱ����ֱ��AD��ֱ��m�ӵױ�BC��������ÿ��2cm���ٶ���DA��������ƽ�ƣ��ֱ�AB��AC��AD��E��F��H������P�����Cʱ����P��ֱ��mͬʱֹͣ�˶������˶�ʱ��Ϊt�루t��0������1����t=2ʱ������DE��DF����֤���ı���AEDFΪ���Σ�
��2���������˶������У����γɵġ�PEF������������ֵ������PEF��������ʱ�����߶�BP�ij���
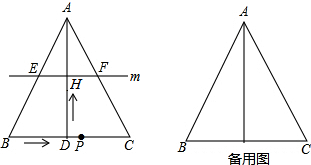
���� ��1�����ͼ1��ʾ���������εĶ���֤����
��2�����ͼ2��ʾ�����������PEF������ı���ʽ��Ȼ�����ö��κ�����������⣮
��� �� 1��֤������t=2ʱ��DH=AH=4����HΪAD���е㣬���ͼ1��ʾ��
1��֤������t=2ʱ��DH=AH=4����HΪAD���е㣬���ͼ1��ʾ��
�֡�EF��AD��
��EFΪAD�Ĵ�ֱƽ���ߣ�
��AE=DE��AF=DF��
��AB=AC��AD��BC�ڵ�D��
��AD��BC����B=��C��
��EF��BC��
���AEF=��B����AFE=��C��
���AEF=��AFE��
��AE=AF��
��AE=AF=DE=DF�����ı���AEDFΪ���Σ�
��2���⣺���ͼ2��ʾ���ɣ�1��֪EF��BC��
���AEF�ס�ABC��
��$\frac{EF}{BC}=\frac{AH}{AD}$����$\frac{EF}{10}=\frac{8-2t}{8}$��
��ã�EF=10-$\frac{5}{2}$t��
S��PEF=$\frac{1}{2}$EF•DH=$\frac{1}{2}$��10-$\frac{5}{2}$t��•2t=-$\frac{5}{2}$t2+10t=-$\frac{5}{2}$��t-2��2+10��0��t��$\frac{10}{3}$����
�൱t=2��ʱ��S��PEF�������ֵ�����ֵΪ10cm2����ʱBP=3t=6cm��
���� �������˶����ۺ��⣬�漰�����붯�������˶����ͣ��ڣ�1���ʿ��������εĶ��壻�ڣ�2���ʿ��������������Ρ�ͼ����������κ����ļ�ֵ���������������ε����ʱ�ʾ��EF�ij��ǽ���Ĺؼ���

 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�| A�� | $\sqrt{20}=2\sqrt{10}$ | B�� | $\sqrt{9}=��3$ | C�� | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | D�� | $\sqrt{��-5��^{2}}$=5 |
| A�� | ��a+b��2=a2+b2 | B�� | a2-b2=��a-b��2 | C�� | ��2x��3=6x3 | D�� | x5��x3=x2 |
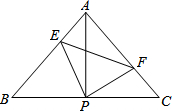 ��֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�������������ĸ����ۣ�
��֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�������������ĸ����ۣ�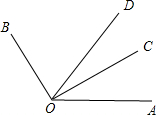 ��ͼ����֪��BOC=2��AOC��ODƽ�֡�AOB���ҡ�AOC=40�㣮
��ͼ����֪��BOC=2��AOC��ODƽ�֡�AOB���ҡ�AOC=40�㣮