题目内容
20. 已知,如图,EF∥AB,DG∥AC,BG=FC,求证:DE∥BC.
已知,如图,EF∥AB,DG∥AC,BG=FC,求证:DE∥BC.
分析 根据平行线分线段成比例定理求出$\frac{CF}{BF}$=$\frac{CE}{AE}$,$\frac{BG}{CG}$=$\frac{BD}{AD}$,求出$\frac{BD}{AD}$=$\frac{CE}{AE}$,$\frac{AB}{AD}$=$\frac{AC}{AE}$,根据相似三角形的判定得出△ADE∽△ABC,根据相似三角形的性质得出∠ADE=∠B,根据平行线的判定得出即可.
解答 证明:∵BG=FC,
∴BF=CG,
∵EF∥AB,DG∥AC,
∴$\frac{CF}{BF}$=$\frac{CE}{AE}$,$\frac{BG}{CG}$=$\frac{BD}{AD}$,
∴$\frac{BD}{AD}$=$\frac{CE}{AE}$,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$,
∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.
点评 本题考查了平行线分线段成比例定理,相似三角形的性质和判定,平行线的判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
10.某班组织了一次经典诵读比赛,男女生各5人组成甲、乙两队参与比赛,成绩如表(10分制):
(1)甲队成绩的平均数是9分,乙队成绩的平均数是9分;
(2)分别计算两队成绩的方差;
(3)根据(1)、(2)计算的结果,你认为那一队的成绩较好,并说明理由.
| 甲队 | 8 | 10 | 9 | 9 | 9 |
| 乙队 | 10 | 8 | 8 | 10 | 9 |
(2)分别计算两队成绩的方差;
(3)根据(1)、(2)计算的结果,你认为那一队的成绩较好,并说明理由.
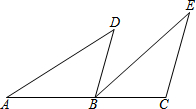 已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB.
已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB. 如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.
如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$. △ABC中,l垂直平分AB交AC于P,交AB于Q,△ABC周长为26cm,AQ=4cm,求△PCB的周长.
△ABC中,l垂直平分AB交AC于P,交AB于Q,△ABC周长为26cm,AQ=4cm,求△PCB的周长.