Question

20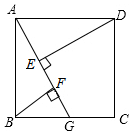．已知：在正方形ABCD中，点G是BC边上的任意一点，DE⊥AG于点E，BF∥DE，交AG于点F． 求证：
（1）△ADE≌△BAF；
（2）AF=BF+EF．

Answer 1

分析 （1）由正方形的性质可知：AD=AB，又因为∠BAF+∠ABF=∠BAF+∠DAE=90°，从而可知∠ABF=∠DAE，然后证明△ADE≌△BAF即可．
（2）由全等三角形的性质可知：BF=AE，可知AF=AE+EF=BF+EF

解答 解：（1）由正方形的性质可知：AD=AB，
∵∠BAF+∠ABF=∠BAF+∠DAE=90°，
∴∠ABF=∠DAE，
在△ADE与△BAF中，
$\left\{\begin{array}{l}{∠DAE=∠ABF}\\{∠AED=∠BFA}\\{AD=AB}\end{array}\right.$
∴△ADE≌△BAF（AAS）
（2）由（1）可知：BF=AE，
∴AF=AE+EF=BF+EF

点评 本题考查正方形的心在，涉及全等三角形的性质与判定，等量代换等知识，解题的关键是证明∠ABF=∠DAE成立，从而可证△ADE≌△BAF成立．