题目内容
9.设[a]表示不超过a的最大整数,例如:[2.3]=2,[-4$\frac{1}{3}$]=-5,[5]=5.(1)求[2$\frac{1}{5}$]+[-3.6]-[-7]的值;
(2)令{a}=a-[a],求{2$\frac{3}{4}$}-[-2.4]+{-6$\frac{1}{4}$}.
分析 (1)根据新定义得:[2$\frac{1}{5}$]=2,[-3.6]=-4,[-7]=-7,再代入计算即可;
(2)根据新定义得:{2$\frac{3}{4}$}=2$\frac{3}{4}$-[2$\frac{3}{4}$]=2$\frac{3}{4}$-2,[-2.4]=-3,{-6$\frac{1}{4}$}=-6$\frac{1}{4}$-[-6$\frac{1}{4}$]=-6$\frac{1}{4}$+7,再代入原式进行计算.
解答 解:(1)[2$\frac{1}{5}$]+[-3.6]-[-7],
=2+(-4)-(-7),
=2-4+7,
=5;
(2){2$\frac{3}{4}$}-[-2.4]+{-6$\frac{1}{4}$},
=2$\frac{3}{4}$-[2$\frac{3}{4}$]-[-2.4]+(-6$\frac{1}{4}$)-[-6$\frac{1}{4}$],
=$\frac{11}{4}$-2+3-$\frac{25}{4}$+7,
=8-$\frac{14}{4}$,
=8-3.5,
=4.5.
点评 本题考查了新定义的理解应用问题以及有理数的混合计算、有理数的大小比较,明确不超过就是小于或等于,即“≤”,认真领会新定义,并能根据新定义化成一般的有理数混合计算的式子,再计算.

练习册系列答案
相关题目
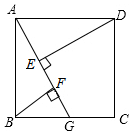 已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证:
已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证: 如图,已知图象x和直线l,以直线l为对称轴,图形x的轴对称图形是( )
如图,已知图象x和直线l,以直线l为对称轴,图形x的轴对称图形是( )



 如图,P是等边三角形ABC内的一点,连结PA、PB、PC,将PB绕B点逆时针旋转60度得到BM,连结MP、MC.
如图,P是等边三角形ABC内的一点,连结PA、PB、PC,将PB绕B点逆时针旋转60度得到BM,连结MP、MC. 如图,已知⊙A与⊙B、⊙C内切,⊙B与⊙C外切,且AB=2,AC=4,BC=4,求⊙A、⊙B、⊙C的半径.
如图,已知⊙A与⊙B、⊙C内切,⊙B与⊙C外切,且AB=2,AC=4,BC=4,求⊙A、⊙B、⊙C的半径. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,