Question

13．如图，在菱形纸片ABCD中，∠A=60°，点E在BC边上，将菱形纸片ABCD沿DE折叠，点C落在AB边的垂直平分线上的点C′处，则∠DEC的大小为（　　）

• A． 30°
• B． 45°
• C． 60°
• D． 75°

Answer 1

分析 连接BD，由菱形的性质及∠A=60°，得到三角形ABD为等边三角形，P为AB的中点，利用三线合一得到DP为角平分线，得到∠ADP=30°，∠ADC=120°，∠C=60°，进而求出∠PDC=90°，由折叠的性质得到∠CDE=∠PDE=45°，利用三角形的内角和定理即可求出所求角的度数．

解答 解：连接BD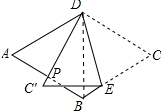，如图所示：
∵四边形ABCD为菱形，
∴AB=AD，
∵∠A=60°，
∴△ABD为等边三角形，∠ADC=120°，∠C=60°，
∵P为AB的中点，
∴DP为∠ADB的平分线，即∠ADP=∠BDP=30°，
∴∠PDC=90°，
∴由折叠的性质得到∠CDE=∠PDE=45°，
在△DEC中，∠DEC=180°-（∠CDE+∠C）=75°．
故选：D．

点评 此题考查了翻折变换（折叠问题），菱形的性质，等边三角形的性质，以及内角和定理，熟练掌握折叠的性质是解本题的关键．