题目内容
18.解方程:(1)2x2-x-2=0.
(2)x2+4x-12=0.
(3)2(x+2)2=x2-4
(4)x2+3x+4=0.
分析 (1)直接利用公式法求出方程的根即可;
(2)利用十字相乘法分解因式解方程即可;
(3)利用平方差公式分解因式,进而结合提取公因式法分解因式解方程;
(4)利用公式法判断b2-4ac的符号,进而得出答案.
解答 解:(1)2x2-x-2=0
∵b2-4ac=1+4×2×2=17,
∴此方程有两个不相等的实数根,
∴x=$\frac{1±\sqrt{17}}{4}$,
则x1=$\frac{1+\sqrt{17}}{4}$,x2=$\frac{1-\sqrt{17}}{4}$;
(2)x2+4x-12=0
(x+6)(x-2)=0,
解得:x1=-6,x2=2;
(3)2(x+2)2=x2-4
2(x+2)-(x+2)(x-2)=0,
(x+2)[2-(x-2)]=0,
解得:x1=-2,x2=4;
(4)x2+3x+4=0
∵b2-4ac=9-4×4×1=-7,
∴此方程没有实数根.
点评 此题主要考查了公式法以及因式分解法解方程,正确分解因式是解题关键.

练习册系列答案
相关题目
13.在平面直角坐标系中,已知点P0的坐标为(1,0).将点P0绕着原点O按顺时针方向旋转45°得点P1,延长OP1到点P2,使OP2=2OP1;再将点P2绕着原点O按顺时针方向旋转45°得点P3,延长OP3到点P4,使OP4=2OP3,…,如此进行下去,则线段OP2014的长为( )
| A. | 22014 | B. | 22013 | C. | 21007 | D. | 21006 |
3.两条对角线垂直且相等的四边形是( )
| A. | 矩形 | B. | 菱形 | ||
| C. | 正方形 | D. | 以上答案均不正确 |
10.在平面直角坐标系xOy中,已知点A(0,1),B(1,2),点P在x轴上运动,当点P到A、B两点距离之差的绝对值最大时,点P的坐标是( )
| A. | (-1,0) | B. | (-2,0) | C. | (0,0) | D. | (1,0) |
8.若(x-5)2=x2+kx+25,则k=( )
| A. | 5 | B. | -5 | C. | 10 | D. | -10 |
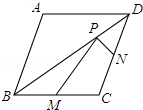 已知菱形ABCD的两条对角线分别为5和12,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=6.5.
已知菱形ABCD的两条对角线分别为5和12,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=6.5.