题目内容
7.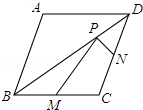 已知菱形ABCD的两条对角线分别为5和12,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=6.5.
已知菱形ABCD的两条对角线分别为5和12,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=6.5.
分析 作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、BP,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
解答 解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP、AC.
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,即Q在AB上.
∵MQ⊥BD,
∴AC∥MQ.
∵M为BC中点,
∴Q为AB中点.
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN.
∴四边形BQNC是平行四边形.
∴NQ=BC.
∵四边形ABCD是菱形,
∴CP=$\frac{1}{2}$AC=2.5,BP=$\frac{1}{2}$BD=6.
在Rt△BPC中,由勾股定理得:BC=$\sqrt{B{P}^{2}+P{C}^{2}}$=6.5,即NQ=6.5,
∴MP+NP=QP+NP=QN=6.5.
故答案为:6.5.
点评 本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P的位置.

练习册系列答案
相关题目
17.已知|m-2|+$\sqrt{n-1}$=0,则方程2m+x=n的解是( )
| A. | x=-4 | B. | x=-3 | C. | x=-2 | D. | x=-1 |
12.下列一组数:-108,6.6,-|-3|,-π,-$\frac{22}{7}$,0.1010010001中,无理数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
16.下列语句正确的是( )
| A. | $\sqrt{24}$是最简二次根式 | B. | $\frac{2}{x}$是分式 | ||
| C. | $\sqrt{9}$=±3 | D. | $\frac{1}{π}$是分式 |
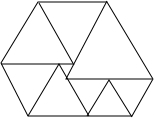 如图,是由9个等边三角形拼成的一个六边形,如果中间最小的等边三角形的边长是1,则此右上角的最大的正三角形的边长是6.
如图,是由9个等边三角形拼成的一个六边形,如果中间最小的等边三角形的边长是1,则此右上角的最大的正三角形的边长是6.