题目内容
 如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行
如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行考点:勾股定理的应用
专题:几何图形问题,转化思想
分析:根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
解答: 解:如图,设大树高为AB=12m,
解:如图,设大树高为AB=12m,
小树高为CD=6m,
过C点作CE⊥AB于E,则四边形EBDC是矩形,
连接AC,
∴EB=6m,EC=8m,AE=AB-EB=12-6=6(m),
在Rt△AEC中,
AC=
=10(m).
故小鸟至少飞行10m.
故答案为:10.
 解:如图,设大树高为AB=12m,
解:如图,设大树高为AB=12m,小树高为CD=6m,
过C点作CE⊥AB于E,则四边形EBDC是矩形,
连接AC,
∴EB=6m,EC=8m,AE=AB-EB=12-6=6(m),
在Rt△AEC中,
AC=
| 62+82 |
故小鸟至少飞行10m.
故答案为:10.
点评:本题考查了勾股定理的应用,根据实际得出直角三角形,培养学生解决实际问题的能力.

练习册系列答案
相关题目
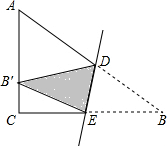 在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.
在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.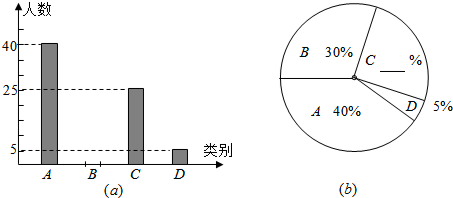

 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形
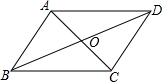
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形 如图,在?ABCD中,已知∠ADO=90°,OA=5cm,OB=3cm,那么AD=
如图,在?ABCD中,已知∠ADO=90°,OA=5cm,OB=3cm,那么AD=