题目内容
12.如果抛物线y=2x2-2ax+2a+1与y=x2-(b-2)x+b的顶点相同,问:自变量x在什么范围内,两函数都随x的增大而增大?分析 把抛物线解析式可化为顶点式,求得两抛物线的顶点坐标,由条件可得到关于a、b的方程组,可求得a、b的值,可求出对称轴,根据二次函数的增减性可得出答案.
解答 解:∵y=2x2-2ax+2a+1=2(x-$\frac{a}{2}$)2+2a+1-$\frac{{a}^{2}}{2}$,y=x2-(b-2)x+b=(x-$\frac{b-2}{2}$)2+b-$\frac{(b-2)^{2}}{4}$,
∴两抛物线的顶点坐标分别为($\frac{a}{2}$,2a+1-$\frac{{a}^{2}}{2}$)、($\frac{b-2}{2}$,$\frac{(b-2)^{2}}{4}$),
∵两抛物线的顶点坐标相同,
∴$\left\{\begin{array}{l}{\frac{a}{2}=\frac{b-2}{2}}\\{2a+1-\frac{{a}^{2}}{2}=b-\frac{(b-2)^{2}}{4}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$.
∴两抛物线的对称轴为x=1,且开口向上,
∴当x≥1时,两函数随x的增大而增大.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式方程是解题的关键.

练习册系列答案
相关题目
7.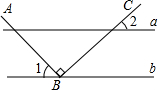 如图所示,直线a∥b,点B在直线b上,且AB∥BC,∠1=55°,则∠2的度数为( )
如图所示,直线a∥b,点B在直线b上,且AB∥BC,∠1=55°,则∠2的度数为( )
 如图所示,直线a∥b,点B在直线b上,且AB∥BC,∠1=55°,则∠2的度数为( )
如图所示,直线a∥b,点B在直线b上,且AB∥BC,∠1=55°,则∠2的度数为( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
1.下列等式正确的是( )
| A. | 3-2=-9 | B. | -0.000000137=-1.37×107 | ||
| C. | (a2)-3=$\frac{1}{{a}^{6}}$ | D. | -$\frac{x-1}{x-y}$=$\frac{x+1}{x-y}$ |
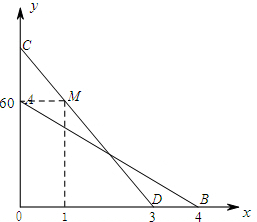 如图,线段AB、CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.
如图,线段AB、CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.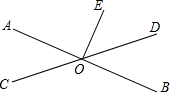 如图,直线AB,CD相交于点O,OE⊥AB于点O,∠COB=145°,则∠DOE=55°.
如图,直线AB,CD相交于点O,OE⊥AB于点O,∠COB=145°,则∠DOE=55°.