题目内容
16.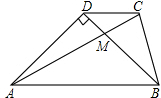 如图所示,在梯形ABCD中,AB∥CD,两对角线交于M,若AD=BD,AC=AB,∠ADB=90°,试说明:
如图所示,在梯形ABCD中,AB∥CD,两对角线交于M,若AD=BD,AC=AB,∠ADB=90°,试说明:(1)∠CAB=30°;
(2)BM=BC.
分析 (1)根据梯形的性质,过点D、C作边AB的垂线,在△ADB中和△ABC中,利用题中的已知条件和直角三角形的性质来证明∠CAB=30°;
(2)利用(1)的结论,在△ABC和△CMB中找∠ACB=∠BMC,等角对等边来证明BM=BC.
解答 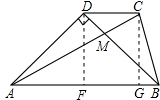 证明:(1)过D作DF⊥AB交AB于点F,过C作CG⊥AB交AB于点G,则DF∥CG,
证明:(1)过D作DF⊥AB交AB于点F,过C作CG⊥AB交AB于点G,则DF∥CG,
∵DC∥AB,
∴DF=CG;
在△ADB中,BD=AD,∠ADB=90°,
∴DF是边AB的中垂线,
∴DF=$\frac{1}{2}$AB,
∴CG=$\frac{1}{2}$AB;
在△ABC中,∵AC=AB,
∴CG=$\frac{1}{2}$AC,
∴∠CAB=30°;
(2)∵在△ABC中,∠CAB=30°,AC=AB,
∴∠ABC=∠ACB=$\frac{1}{2}$×(180-30)=75°;
∵在△ADB中,BD=AD,∠ADB=90°,
∴∠DAB=45°,∠DBA=∠DAB=45°,
∵∠CAB=30°,
∴∠CMB=45°+30°=75°,
∴∠ACB=∠BMC,
∴BM=BC.
点评 本题考查的是梯形的性质,等腰直角三角形的性质,等腰三角形的判定与性质,平行线之间的距离处处相等的性质,三角形内角和定理以及外角的性质,
综合性较强,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
相关题目
7. 如图,A、B、C三点在⊙O上,∠ACB=30°,则∠AOB的度数( )
如图,A、B、C三点在⊙O上,∠ACB=30°,则∠AOB的度数( )
 如图,A、B、C三点在⊙O上,∠ACB=30°,则∠AOB的度数( )
如图,A、B、C三点在⊙O上,∠ACB=30°,则∠AOB的度数( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
1.已知a、b是两个连续的整数,且a<$\sqrt{15}$<b,则a+b等于( )
| A. | 5 | B. | 6 | C. | 7 | D. | 6.5 |
8. 如图,用尺规作出∠AOB的角平分线OE,在作角平分线过程中,用到的三角形全等的判定方法是( )
如图,用尺规作出∠AOB的角平分线OE,在作角平分线过程中,用到的三角形全等的判定方法是( )
 如图,用尺规作出∠AOB的角平分线OE,在作角平分线过程中,用到的三角形全等的判定方法是( )
如图,用尺规作出∠AOB的角平分线OE,在作角平分线过程中,用到的三角形全等的判定方法是( )| A. | ASA | B. | SSS | C. | SAS | D. | AAS |
 对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把
对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把