题目内容
选做题:请你从甲、乙两题中任选一题作答,如果两题都做,只以甲题计分.
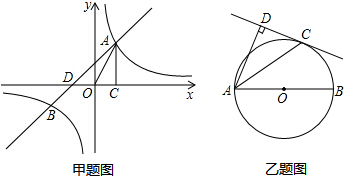
甲题:如图,已知反比例函数y1=
(k1>0)与一次函数y2=k2x+1 (k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
乙题:如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD=4,求AC的长.
甲题:如图,已知反比例函数y1=
| k1 |
| x |
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
乙题:如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD=4,求AC的长.

考点:切线的判定,反比例函数与一次函数的交点问题
专题:
分析:甲题:(1)先求出AC=2OC,根据三角形面积求出A的坐标,代入函数的解析式求出即可;
(2)求出B的坐标,根据A、B的坐标结合图象得出即可;
乙题:(1)连接OC,求出OC和AD平行,推出OC⊥DC,根据切线的判定得出即可;
(2)证△DAC和△CAB相似,得出比例式,代入求出即可.
(2)求出B的坐标,根据A、B的坐标结合图象得出即可;
乙题:(1)连接OC,求出OC和AD平行,推出OC⊥DC,根据切线的判定得出即可;
(2)证△DAC和△CAB相似,得出比例式,代入求出即可.
解答:甲题解:(1)在Rt△OAC中,设OC=m,
∵tan∠AOC=
=2,
∴AC=2×OC=2m,
∵S△AOC=
×OC×AC=
×m×2m=1,
∴m2=1,
∴m=1或m=-1(舍去),
∴m=1,
∴A点的坐标为(1,2),
把A点的坐标代入y1=
中,得k1=2,
∴反比例函数的表达式为y1=
,
把A点的坐标代入y2=k2x+1,得k2=1,
∴一次函数的表达式是y2=x+1;
(2)B点的坐标为(-2,-1),
当0<x<1或x<-2时,y1>y2.

乙题(1)证明:如图,连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
又∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥DC,
∴OC⊥DC,
∴DC为⊙O的切线.
(2)解:连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
又∵AD⊥DC,
∴∠ADC=90°,
∴∠ACB=∠ADC,
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∴△ABC∽△ACD,
∴
=
,
∴AC2=AB•AD,
∵AB=2×3=6,AD=4,
∴AC=2
.
∵tan∠AOC=
| AC |
| OC |
∴AC=2×OC=2m,
∵S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴m2=1,
∴m=1或m=-1(舍去),
∴m=1,
∴A点的坐标为(1,2),
把A点的坐标代入y1=
| k1 |
| x |
∴反比例函数的表达式为y1=
| 2 |
| x |
把A点的坐标代入y2=k2x+1,得k2=1,
∴一次函数的表达式是y2=x+1;
(2)B点的坐标为(-2,-1),
当0<x<1或x<-2时,y1>y2.

乙题(1)证明:如图,连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
又∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥DC,
∴OC⊥DC,
∴DC为⊙O的切线.
(2)解:连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
又∵AD⊥DC,
∴∠ADC=90°,
∴∠ACB=∠ADC,
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∴△ABC∽△ACD,
∴
| AB |
| AC |
| AC |
| AD |
∴AC2=AB•AD,
∵AB=2×3=6,AD=4,
∴AC=2
| 6 |
点评:本题考查了一次函数和反比例函数的交点问题,切线的判定,相似三角形的性质和判定的应用,主要考查学生运用定理和性质进行推理和计算的能力,题目比较好,难度适中.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论: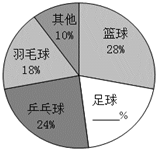 某校课外活动小组为了了解学生最喜欢的球类运动的情况,随机抽查了该校学生,调查数据整理如图,请根据扇形统计图解答以下问题:
某校课外活动小组为了了解学生最喜欢的球类运动的情况,随机抽查了该校学生,调查数据整理如图,请根据扇形统计图解答以下问题: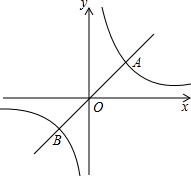 如图,定义:若双曲线y=
如图,定义:若双曲线y= 已知如图,AB∥CD,直线l分别截AB、CD于P、C两点,PE平分∠BPC交CD于点E,PF平分∠BPE交CD于点F.若∠PCD=α°,则∠PFC=
已知如图,AB∥CD,直线l分别截AB、CD于P、C两点,PE平分∠BPC交CD于点E,PF平分∠BPE交CD于点F.若∠PCD=α°,则∠PFC=