题目内容
16.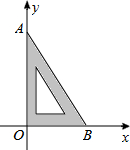 如图,把含有30°角的三角板ABO置入平面直角坐标系中,AB=4,则点A的坐标为(0,2$\sqrt{3}$).
如图,把含有30°角的三角板ABO置入平面直角坐标系中,AB=4,则点A的坐标为(0,2$\sqrt{3}$).
分析 因为点A在y轴上,所以横坐标为0,利用已知条件求出OA的长即可得到其纵坐标,问题得解.
解答 解:
∵∠AOB=90°,AB=4,∠OAB=30°,
∴OB=$\frac{1}{2}$AB=2,
∴AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=2$\sqrt{3}$,
∴点A的坐标是(0,2$\sqrt{3}$),
故答案为:(0,2$\sqrt{3}$).
点评 本题考查了勾股定理的运用以及含30°直角的直角三角形的性质,利用勾股定理求出OA的长是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.计算:$\sqrt{3}×\sqrt{6}$的结果是( )
| A. | $9\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{6}$ |
6.从2,-2,1,-1四个数中任取2个不同的数求和,其和为1的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
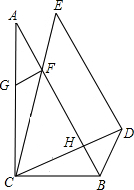 如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号).
如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号).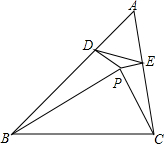 如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.
如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.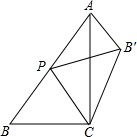 如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是2.
如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是2.